Hvordan er acceleration af forskellige typer angivet i fysik? Et eksempel på et accelerationsproblem

2024 Forfatter: Angel Austin | [email protected]. Sidst ændret: 2023-12-17 05:21

Når de studerer i fysik den mekaniske bevægelse af legemer i rummet, tager de altid højde for den resulterende acceleration. Lad os i artiklen overveje, hvad acceleration er, og hvordan det betegnes i fysik, og også løse et simpelt problem for at beregne denne værdi.

Hvad er acceleration, og hvad er dens typer?

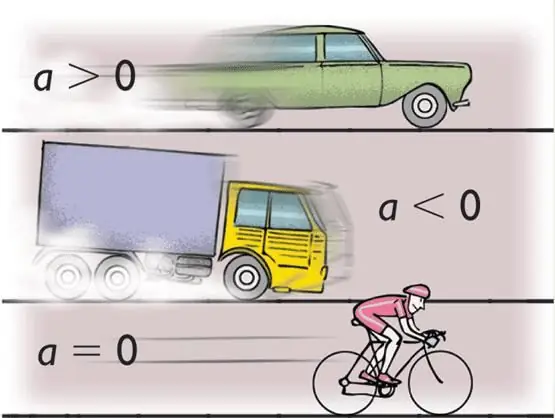
Under accelerationen forstå værdien, hvis betydning er hastigheden af ændringer i kroppens hastighed. Matematisk er denne definition skrevet som følger:

a=dv/dt.

Hvis tidsfunktionen af hastighed er kendt, så er det nok at finde dens første afledede for at beregne accelerationen på et givet tidspunkt.

I fysik er accelerationsbogstavet det små latinske a. Dette er dog den såkaldte lineære acceleration, som måles i m/s². Ud over det er der også vinkelacceleration. Den viser ændringen i vinkelhastighed og udtrykkes i enheder af rad/s². Denne type acceleration er angivet med det græske lille bogstav α (alfa). Sommetiderbogstavet ε (epsilon) bruges til at betegne det.

Hvis kroppen bevæger sig langs en buet bane, opdeles den totale acceleration i to komponenter: tangentiel (bestemmer ændringen i hastighed i størrelse) og normal (bestemmer ændringen i hastighed i retning). Disse typer af acceleration er også angivet med bogstaverne a, men ved hjælp af de tilsvarende indekser: a_t og a. Normal kaldes ofte centripetal, og tangential kaldes ofte tangent.

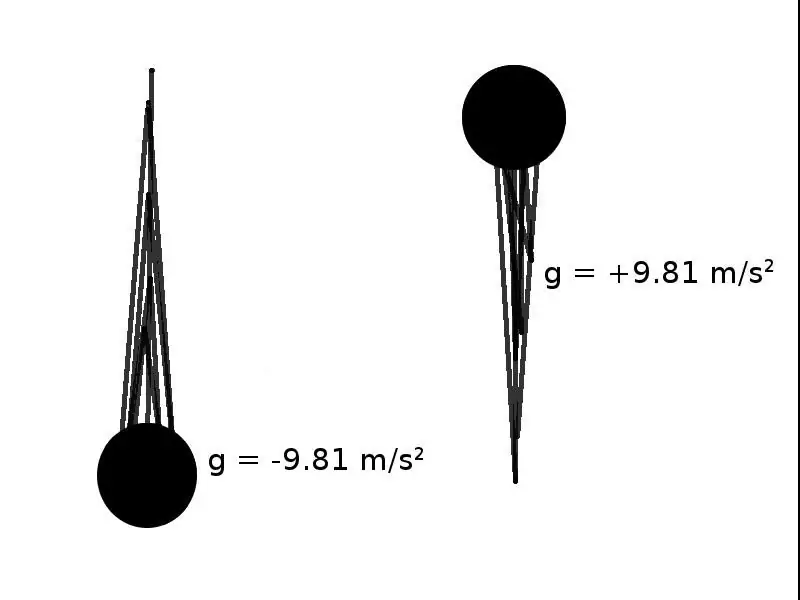
Endelig er der en anden type acceleration, der opstår, når kroppe falder frit i planetens gravitationsfelt. Det er angivet med bogstavet g.

Problem i fysik til acceleration

Det er kendt, at kroppen bevæger sig i en lige linje. Dens hastighed over tid bestemmes af følgende lov:

v=2t²-t+4.

Det er nødvendigt at beregne den acceleration, som kroppen vil have til tiden t=2,5 sekunder.

Efter definitionen af a får vi:

a=dv/dt=4t - 1.

Det vil sige, at værdien a afhænger lineært af tiden. Det er besynderligt at bemærke, at i det indledende øjeblik (t=0) var accelerationen negativ, det vil sige rettet mod hastighedsvektoren. Vi får svaret på problemet ved at indsætte t=2,5 sekunder i denne ligning: a=9 m/s².