Hver person i løbet af sit liv møder kroppe, der er i en af de tre samlede tilstande af stof. Den enkleste aggregeringstilstand at studere er gas. I artiklen vil vi overveje begrebet en ideel gas, give systemets tilstandsligning og også være opmærksom på beskrivelsen af den absolutte temperatur.
Gassens tilstand
Hver elev har en god idé om, hvilken stoftilstand de taler om, når de hører ordet "gas". Dette ord forstås som en krop, der er i stand til at optage et hvilket som helst volumen, der leveres til det. Den er ikke i stand til at holde sin form, fordi den ikke kan modstå selv den mindste ydre påvirkning. Gas bevarer heller ikke volumen, hvilket adskiller den ikke kun fra faste stoffer, men også fra væsker.
Ligesom en væske er en gas et flydende stof. I processen med bevægelse af faste legemer i gasser hæmmer sidstnævnte denne bevægelse. Den resulterende kraft kaldes modstand. Dens værdi afhænger afkroppens hastighed i gassen.
Stærke eksempler på gasser er luft, naturgas til opvarmning af boliger og madlavning, inaktive gasser (Ne, Ar), der bruges til at fylde reklamegløderør eller bruges til at skabe et inert (ikke-aggressivt, beskyttende) miljø ved svejsning.
Ideel gas
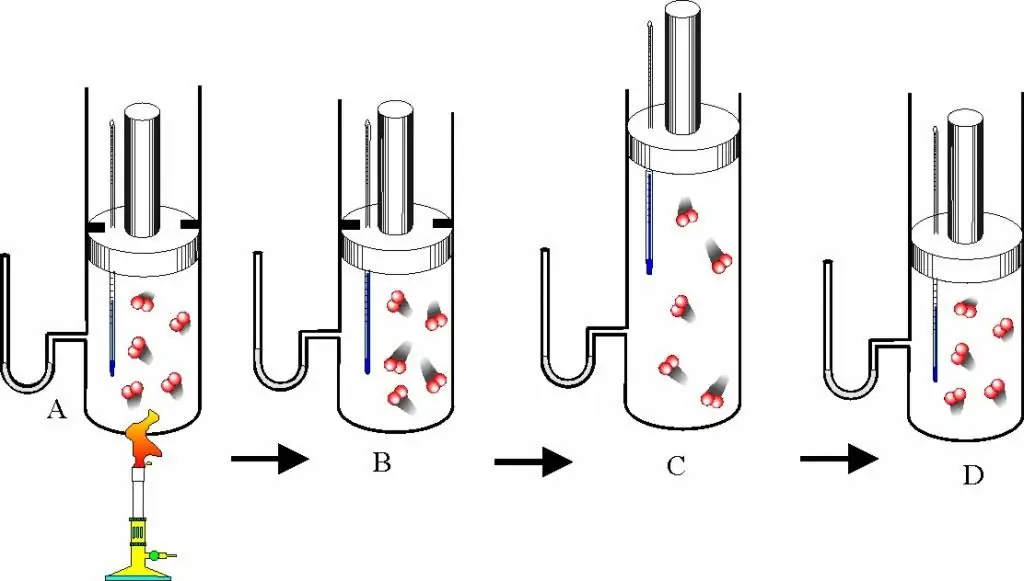
Før du går videre til beskrivelsen af gaslove og tilstandsligningen, bør du godt forstå spørgsmålet om, hvad en ideel gas er. Dette koncept introduceres i molekylær kinetisk teori (MKT). En ideel gas er enhver gas, der opfylder følgende egenskaber:
- Partiklerne, der danner det, interagerer ikke med hinanden undtagen ved direkte mekaniske kollisioner.
- Som et resultat af partiklernes kollision med fartøjets vægge eller indbyrdes bevares deres kinetiske energi og momentum, det vil sige, at kollisionen betragtes som absolut elastisk.
- Partikler har ingen dimensioner, men har en endelig masse, det vil sige, at de ligner materialepunkter.
Det er naturligt, at enhver gas ikke er ideel, men ægte. Ikke desto mindre er disse tilnærmelser ganske gyldige og kan bruges til at løse mange praktiske problemer. Der er en generel empirisk regel, der siger: uanset den kemiske natur, hvis en gas har en temperatur over stuetemperatur og et tryk i størrelsesordenen atmosfærisk eller lavere, så kan den betragtes som ideel med høj nøjagtighed og kan bruges til at beskrive det.formel for den ideelle gasligning for tilstand.
Clapeyron-Mendeleev lov
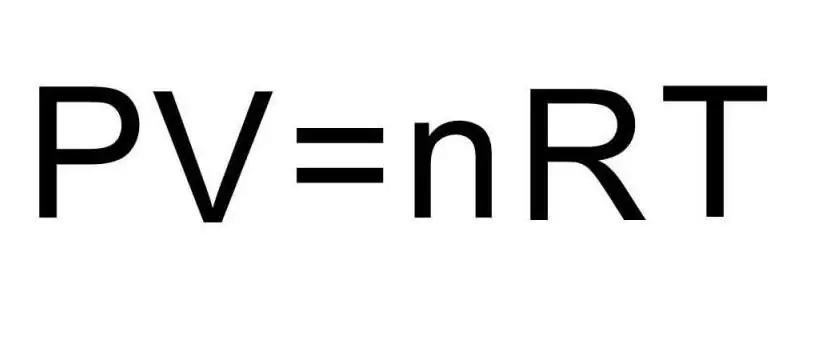
Overgange mellem forskellige aggregerede tilstande af stof og processer inden for en enkelt aggregeret tilstand håndteres af termodynamik. Tryk, temperatur og volumen er tre størrelser, der unikt definerer enhver tilstand i et termodynamisk system. Formlen for tilstandsligningen for en ideel gas kombinerer alle tre af disse størrelser til en enkelt lighed. Lad os skrive denne formel:
PV=nRT
Her P, V, T - henholdsvis tryk, volumen, temperatur. Værdien af n er mængden af stof i mol, og symbolet R angiver den universelle konstant for gasser. Denne lighed viser, at jo større produktet af tryk og volumen er, desto større må produktet være af mængden af stof og temperatur.

Formlen for tilstandsligningen for en gas kaldes Clapeyron-Mendeleev-loven. I 1834 kom den franske videnskabsmand Emile Clapeyron, som opsummerede sine forgængeres eksperimentelle resultater, til denne ligning. Clapeyron brugte dog en række konstanter, som Mendeleev senere erstattede med en - den universelle gaskonstant R (8, 314 J / (molK)). Derfor er denne ligning i moderne fysik opkaldt efter navnene på franske og russiske videnskabsmænd.

Andre ligningsformer
Ovenfor skrev vi Mendeleev-Clapeyrons tilstandsligning for en ideel gas i det generelt accepterede ogbekvem form. Ved problemer inden for termodynamik kan det dog ofte være nødvendigt med en lidt anden form. Der er skrevet yderligere tre formler nedenfor, som følger direkte af den skrevne ligning:
PV=NkBT;
PV=m/MRT;
P=ρRT/M.
Disse tre ligninger er også universelle for en ideel gas, kun i dem optræder sådanne mængder som masse m, molær masse M, massefylde ρ og antallet af partikler N, der udgør systemet. Symbolet kB her angiver Boltzmann-konstanten (1, 3810-23J/K).
Boyle-Mariotte Law
Da Clapeyron udarbejdede sin ligning, var han baseret på gaslove, der var blevet opdaget eksperimentelt adskillige årtier tidligere. En af dem er Boyle-Mariotte-loven. Det afspejler en isoterm proces i et lukket system, som et resultat af hvilken makroskopiske parametre som tryk og volumen ændrer sig. Hvis vi sætter T og n konstant i tilstandsligningen for en ideel gas, så vil gasloven antage formen:
P1V1=P2V 2
Dette er Boyle-Mariotte-loven, som siger, at produktet af tryk og volumen bevares under en vilkårlig isoterm proces. I dette tilfælde ændres selve værdierne P og V.
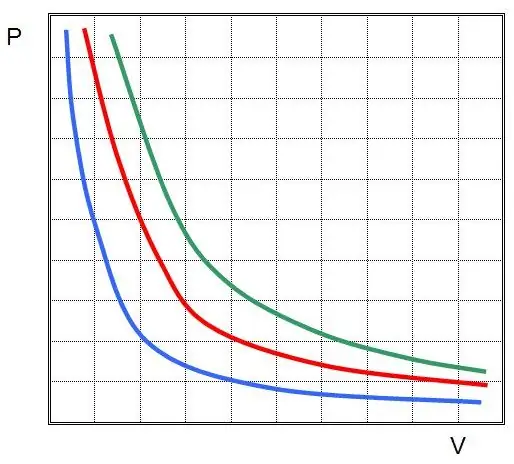
Hvis du plotter P(V) eller V(P), vil isotermerne være hyperbler.
Charles og Gay-Lussacs love
Disse love beskriver matematisk isobarisk og isokoriskprocesser, det vil sige sådanne overgange mellem gassystemets tilstande, hvori henholdsvis tryk og volumen bevares. Charles' lov kan matematisk skrives som følger:
V/T=const når n, P=const.
Gay-Lussacs lov er skrevet som følger:
P/T=const når n, V=const.
Hvis begge ligheder præsenteres i form af en graf, vil vi få rette linjer, der hælder i en eller anden vinkel til x-aksen. Denne type graf angiver en direkte proportionalitet mellem volumen og temperatur ved konstant tryk og mellem tryk og temperatur ved konstant volumen.
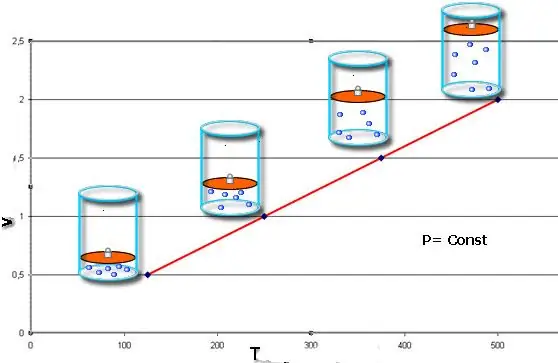
Bemærk, at alle tre betragtede gaslove ikke tager hensyn til gassens kemiske sammensætning såvel som ændringen i dens mængde af stof.
Absolut temperatur
I hverdagen er vi vant til at bruge Celsius-temperaturskalaen, da den er praktisk til at beskrive processerne omkring os. Så vand koger ved 100 oC og fryser ved 0 oC. I fysik viser denne skala sig at være ubelejlig, derfor bruges den såkaldte absolutte temperaturskala, som blev indført af Lord Kelvin i midten af det 19. århundrede. I overensstemmelse med denne skala måles temperaturen i Kelvin (K).
Det menes, at ved en temperatur på -273, 15 oC er der ingen termiske vibrationer af atomer og molekyler, deres fremadgående bevægelse stopper fuldstændigt. Denne temperatur i grader Celsius svarer til det absolutte nulpunkt i Kelvin (0 K). Fra denne definitionden fysiske betydning af absolut temperatur følger: det er et mål for den kinetiske energi af de partikler, der udgør stof, for eksempel atomer eller molekyler.
Udover ovenstående fysiske betydning af absolut temperatur, er der andre tilgange til at forstå denne størrelse. En af dem er Charles nævnte gaslov. Lad os skrive det i følgende form:
V1/T1=V2/T 2=>
V1/V2=T1/T 2.
Den sidste lighed siger, at ved en bestemt mængde stof i systemet (f.eks. 1 mol) og et vist tryk (f.eks. 1 Pa), bestemmer gasvolumenet entydigt den absolutte temperatur. Med andre ord er en stigning i gasvolumenet under disse forhold kun mulig på grund af en stigning i temperaturen, og et fald i volumen indikerer et fald i værdien af T.
Husk på, at i modsætning til Celsius-temperaturen kan den absolutte temperatur ikke være negativ.
Avogadro-princippet og gasblandinger
Ud over de ovennævnte gaslove, fører tilstandsligningen for en ideel gas også til det princip, som Amedeo Avogadro opdagede i begyndelsen af det 19. århundrede, og som bærer hans efternavn. Dette princip fastslår, at volumenet af enhver gas ved konstant tryk og temperatur bestemmes af mængden af stof i systemet. Den tilsvarende formel ser sådan ud:
n/V=const når P, T=const.
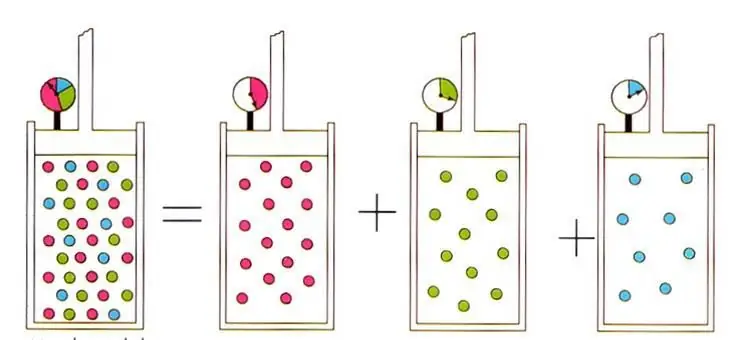
Det skrevne udtryk fører til den velkendte i idealgasfysikken D altons lov for gasblandinger. Detteloven siger, at parti altrykket af en gas i en blanding er entydigt bestemt af dens atomare fraktion.
Eksempel på problemløsning
I en lukket beholder med stive vægge, der indeholder en ideel gas, steg trykket 3 gange som følge af opvarmning. Det er nødvendigt at bestemme den endelige temperatur for systemet, hvis dets startværdi var 25 oC.
Først, lad os konvertere temperaturen fra grader Celsius til Kelvin, vi har:
T=25 + 273, 15=298, 15 K.
Da beholderens vægge er stive, kan opvarmningsprocessen betragtes som isokorisk. I denne sag anvender vi Gay-Lussac-loven, vi har:
P1/T1=P2/T 2=>
T2=P2/P1T 1.
Den endelige temperatur bestemmes således ud fra produktet af trykforholdet og starttemperaturen. Ved at erstatte dataene med lighed får vi svaret: T2=894,45 K. Denne temperatur svarer til 621,3 oC.






