For at kunne afbilde genstande på papir, der i virkeligheden ikke har særlig "praktiske" størrelser, fandt folk på en skala. Faktisk forklarer dette, hvad skalaen er til.
Når skolepensum begynder at afsløre begrebet skala
For første gang støder børn på dette ord, mens de studerer kort og planer over området. Læreren forklarer, hvorfor skalaen er nødvendig, hvad den viser, ved at bruge atlass som eksempel. Det forklares, at ethvert geografisk træk er så stort, at det ville være svært og ubelejligt at afbilde det i fuld størrelse.
Folk tegnede terrænet i en reduceret form, men til dette brugte de ingen nøjagtige forhold. Nu bliver det gjort smartere - hver streg og streg afbildet på kortet har en størrelse, der kan ganges med et bestemt tal og finde ud af den sande længde og bredde.
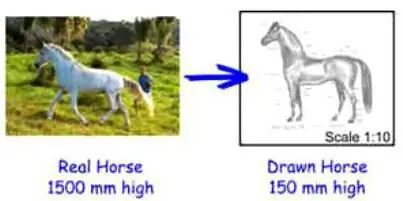
Record-skala: den første måde at læse på
Skalaen er angivet med to tal adskilt af et kolon. Det første ciffer angiver dimensionsenhederne i figuren, det andetangiver, hvor mange reelle enheder i figuren, der svarer til det første tal. For eksempel, hvis en skala på 1:1000 er angivet på en plan, og dimensionsenhederne er angivet i centimeter, svarer en centimeter i figuren til 1000 cm i virkeligheden. Så hvad er skalaen til? Med dens hjælp kan du ikke kun reducere visse objekter på den grafiske plan, men også nøjagtigt beregne deres reelle størrelse.
Den anden måde at optage skalaen på: hvad er praktisk?
Den tidligere metode til at skrive skalaen gennem et kolon kaldes numerisk. Men der er også en navngiven skala. Hans rekord er som følger: 1 cm - 20 km. Det viser sig, at det på denne måde er muligt kompakt at nedskrive enorme skalaer, der ikke vil blive udtrykt med tal med flere nuller, hvis der er opstået en situation, hvor det er nødvendigt at angive flere hundrede kilometer på en centimeter. Samtidig står det umiddelbart klart hvor meget, hvad og i hvad. Denne post er mere intuitiv og klar.
Skalering i tegning: hvad supplerer det tidligere undersøgte koncept
Begrebet skala møder man ikke kun i geografi, men også i studiet af et emne som tegning. De samme principper bruges til at skildre forskellige objekter. Men der er en væsentlig forskel: her udvides begrebet, hvad skala er for, også ved, at det kan bruges til at afbilde små detaljer i større skala. I geografi taler vi ikke om dette, for der er ikke så små genstande i geografien, at der er behov for at forstørre dem. Kontinenter og bjerge, floder og søer er under alle omstændigheder større end ark A4 eller enddaA1.
Når du studerer tegning, kan du bruge skalaen til at afbilde de mindste detaljer i større form, såsom en bolt eller tandhjul.
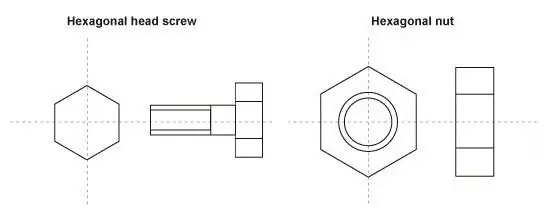
Så hvorfor har vi brug for en vægt i dette tilfælde? Med dens hjælp kan du mere bekvemt, klart og detaljeret afbilde et lille element. I dette tilfælde sker det omvendte i notationen: det første tal vil være større end det andet, og notationen 100:1 vil lyde sådan her: 100 metriske enheder af billedet svarer til én enhed af den faktiske størrelse.
Et par opklarende eksempler
Hvad er skalaen til, hvad viser den i tilfælde af et billede af en mindre genstand, hvilket er resultatet på papir? Igen har vi det nøjagtige forhold mellem dimensionerne af billedet af delen og det virkelige objekt. Husk den samme skala på 100:1. Det viser sig, at i hundrede millimeter i figuren er der kun en millimeter af reel størrelse. Hvis en del er 500 millimeter bred på billedet, er dens faktiske bredde kun 5 millimeter.
Hvis vi husker det første tilfælde, billedet på et ark af en mindre kopi af et stort objekt, vil skalaen 1:100 betyde, at en millimeter i billedet indeholder 100 millimeter af den sande størrelse. Så hvis et objekt er 80 millimeter langt på en tegning eller et kort, vil den faktiske længde af objektet være 8000 millimeter. Et tydeligt eksempel på, hvad skala er for, og hvilken bekvem opfindelse af menneskeheden.
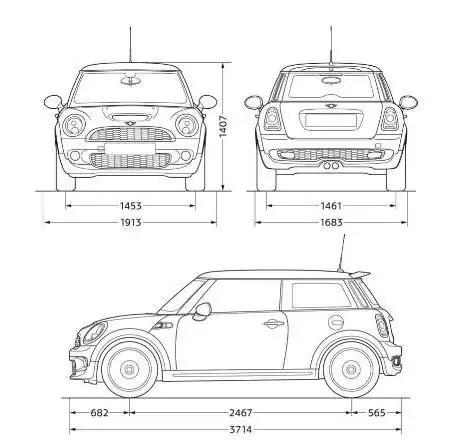
Det vigtigste ved at bruge skalaen er strakshusk, at det første tal refererer til billedet og det andet til objekternes faktiske størrelse. For ikke at blive forvirret i fremtiden, for at konsolidere disse fundamenter, afholdes praktiske klasser i geografi i skolerne, så børn forklarer og beregner størrelsen af rigtige objekter flere gange ved hjælp af atlasset. Det samme sker i tegnetimer.
Summarize
Hvad er skalaen til? Svaret på dette spørgsmål består af tre punkter, som du bare skal huske:
- Først - skalaen er nødvendig for at vise store genstande på en overflade, der er praktisk at se.
- For det andet - skalaen er nødvendig for at afbilde små objekter i en større størrelse.
- Tredje - skalaen er nødvendig for nøjagtigt at kunne bestemme størrelsen af et rigtigt objekt, uanset dets oprindelige størrelse, lille eller stor.






