I denne artikel betragtes metoden som en måde at løse systemer af lineære ligninger (SLAE). Metoden er analytisk, det vil sige den giver dig mulighed for at skrive en generel løsningsalgoritme og derefter erstatte værdier fra specifikke eksempler der. I modsætning til matrixmetoden eller Cramers formler kan man, når man løser et system af lineære ligninger ved hjælp af Gauss-metoden, også arbejde med dem, der har uendeligt mange løsninger. Eller slet ikke have det.
Hvad vil det sige at løse ved Gauss-metoden?
Først skal vi skrive vores ligningssystem ned som en matrix. Det ser sådan ud. Systemet er taget:
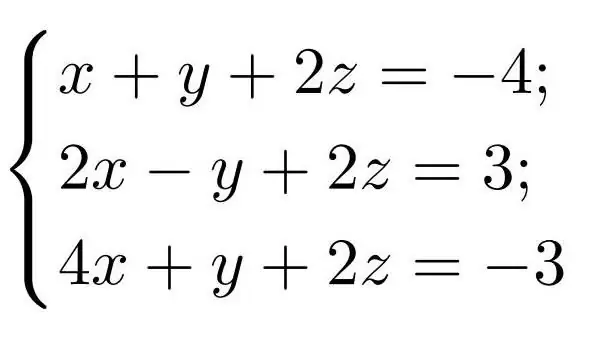
Koefficienter er skrevet i form af en tabel, og til højre i en separat kolonne - gratis medlemmer. Søjlen med frie elementer er adskilt af bekvemmelighed med en lodret streg. En matrix, der inkluderer denne kolonne, kaldes udvidet.

Dernæst skal hovedmatrixen med koefficienter reduceres til den øverste trekantede form. Dette er hovedpunktet i at løse systemet ved Gauss-metoden. Kort sagt, efter visse manipulationer skulle matrixen se sådan ud, så der kun er nuller i dens nederste venstre del:

Så, hvis du skriver den nye matrix igen som et ligningssystem, vil du bemærke, at den sidste linje allerede indeholder værdien af en af rødderne, som så substitueres i ligningen ovenfor, en anden rod findes, og så videre.
Dette er en beskrivelse af den gaussiske løsning i de mest generelle vendinger. Og hvad sker der, hvis systemet pludselig ikke har en løsning? Eller er der et uendeligt antal af dem? For at besvare disse og mange flere spørgsmål er det nødvendigt at overveje separat alle de elementer, der anvendes i løsningen ved Gauss-metoden.
Matricer, deres egenskaber
Der er ingen skjult betydning i matrixen. Det er bare en bekvem måde at registrere data til senere operationer. Selv skolebørn bør ikke være bange for dem.
Matrixen er altid rektangulær, fordi den er mere praktisk. Selv i Gauss-metoden, hvor alt går ud på at bygge en trekantet matrix, dukker et rektangel op i indtastningen, kun med nuller på det sted, hvor der ikke er tal. Nuller kan udelades, men de er underforståede.
Matrix har størrelse. Dens "bredde" er antallet af rækker (m), dens "længde" er antallet af kolonner (n). Så vil størrelsen af matricen A (store latinske bogstaver bruges norm alt til deres betegnelse) betegnes som Am×n. Hvis m=n, så er denne matrix kvadratisk, ogm=n - dens rækkefølge. Følgelig kan ethvert element i matricen A betegnes med nummeret på dens række og kolonne: axy; x - rækkenummer, skift [1, m], y - kolonnenummer, skift [1, n].
I den Gaussiske metode er matricer ikke hovedpunktet i løsningen. I princippet kan alle operationer udføres direkte med selve ligningerne, dog vil notationen være meget mere besværlig, og det vil være meget nemmere at blive forvirret i det.
Qualifier
Matrixen har også en determinant. Dette er en meget vigtig funktion. At finde ud af dens betydning nu er ikke det værd, du kan blot vise, hvordan det beregnes, og derefter fortælle, hvilke egenskaber af matrixen den bestemmer. Den nemmeste måde at finde determinanten på er gennem diagonaler. I matrixen tegnes imaginære diagonaler; elementerne på hver af dem ganges, og derefter tilføjes de resulterende produkter: diagonaler med en hældning til højre - med et "plus"-tegn, med en hældning til venstre - med et "minus"-tegn.
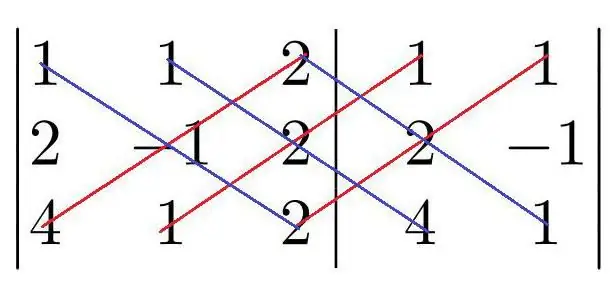
Det er ekstremt vigtigt at bemærke, at determinanten kun kan beregnes for en kvadratisk matrix. For en rektangulær matrix kan du gøre følgende: Vælg den mindste af antallet af rækker og antallet af kolonner (lad det være k), og marker derefter tilfældigt k kolonner og k rækker i matricen. Elementerne placeret i skæringspunktet mellem de valgte kolonner og rækker vil danne en ny firkantet matrix. Hvis determinanten for en sådan matrix er et andet tal end nul, vil det blive kaldt den grundlæggende mol af den oprindelige rektangulære matrix.
Førhvordan man begynder at løse et ligningssystem ved Gauss-metoden, skader det ikke at beregne determinanten. Hvis det viser sig at være nul, så kan vi med det samme sige, at matrixen enten har et uendeligt antal løsninger, eller der er slet ingen. I sådan et trist tilfælde er du nødt til at gå videre og finde ud af matrixens rang.
Klassificering af systemer
Der er sådan noget som rangen af en matrix. Dette er den maksimale rækkefølge af dens ikke-nul determinant (ved at huske basis-moll, kan vi sige, at rangeringen af en matrix er rækkefølgen af basis-moll).
Som tingene er med rang, kan SLOW opdeles i:
- Joint. For fælles systemer falder rangen af hovedmatricen (kun bestående af koefficienter) sammen med rangeringen af den udvidede (med en kolonne med frie udtryk). Sådanne systemer har en løsning, men ikke nødvendigvis én, derfor er fælles systemer yderligere opdelt i:
- - bestemt - at have en unik løsning. I visse systemer er rangeringen af matrixen og antallet af ukendte ens (eller antallet af kolonner, hvilket er det samme);
- - ubestemt - med et uendeligt antal løsninger. Rangeringen af matricer i sådanne systemer er mindre end antallet af ukendte.
- Inkompatibel. For sådanne systemer matcher rækken af hoved- og udvidede matricer ikke. Inkompatible systemer har ingen løsning.
Gauss-metoden er god, fordi den giver dig mulighed for enten at opnå et utvetydigt bevis for systemets inkonsistens (uden at beregne determinanterne for store matricer) eller en generel løsning for et system med et uendeligt antal løsninger.
Elementære transformationer
Førhvordan man går direkte videre til systemets løsning, kan du gøre det mindre besværligt og mere bekvemt til beregninger. Dette opnås gennem elementære transformationer - sådan at deres implementering ikke ændrer det endelige svar på nogen måde. Det skal bemærkes, at nogle af de ovennævnte elementære transformationer kun er gyldige for matricer, hvis kilde netop var SLAE. Her er en liste over disse transformationer:
- Skift strenge. Det er indlysende, at hvis vi ændrer rækkefølgen af ligningerne i systemposten, så vil dette ikke påvirke løsningen på nogen måde. Derfor er det også muligt at bytte rækker i matrixen af dette system, selvfølgelig ikke at glemme kolonnen med gratis medlemmer.
- Multiplikation af alle elementer i en streng med en eller anden faktor. Meget brugbar! Med den kan du reducere store tal i matrixen eller fjerne nuller. Sættet af løsninger vil som sædvanligt ikke ændre sig, og det bliver mere bekvemt at udføre yderligere operationer. Det vigtigste er, at koefficienten ikke skal være lig med nul.
- Slet linjer med proportionalkoefficienter. Dette følger til dels af det foregående afsnit. Hvis to eller flere rækker i matrixen har proportionalkoefficienter, opnås to (eller igen flere) absolut identiske rækker, når du multiplicerer / dividerer en af rækkerne med proportionalitetskoefficienten, og du kan fjerne de ekstra, så der kun er tilbage en.
- Slet nullinjen. Hvis der i løbet af transformationer opnås en streng et sted, hvor alle elementer, inklusive det frie medlem, er nul, så kan en sådan streng kaldes nul og smidt ud af matrixen.
- Tilføjelse til elementerne i en række af elementer i en anden (ifølgetilsvarende kolonner) ganget med en eller anden koefficient. Den mest uklare og vigtigste transformation af alle. Det er værd at dvæle ved det mere detaljeret.
Tilføjelse af en streng ganget med en faktor
For at lette forståelsen er det værd at skille denne proces ad trin for trin. To rækker er taget fra matrixen:
a11 a12 … a1n | b1
a21 a22 … a2n | b2
Lad os sige, at du skal lægge den første ganget med koefficienten "-2" til den anden.
a'21 =a21 + -2×a11
a'22 =a22 + -2×a12
a'2n =a2n + -2×a1n
Derefter erstattes anden række i matrixen med en ny, mens den første forbliver uændret.
a11 a12 … a1n | b1
a'21 a'22 … a'2n | b2
Det skal bemærkes, at multiplikationsfaktoren kan vælges på en sådan måde, at et af elementerne i den nye streng, som et resultat af at tilføje to strenge, er lig nul. Derfor er det muligt at få en ligning i systemet, hvor der vil være en mindre ukendt. Og hvis du får to sådanne ligninger, så kan operationen gøres igen og få en ligning, der allerede vil indeholde to mindre ukendte. Og hvis vi hver gang drejer til nul en koefficient for alle rækker, der er lavere end den oprindelige, så kan vi ligesom trin gå ned til bunden af matricen og få en ligning med en ukendt. Dette kaldesløs systemet ved hjælp af Gauss-metoden.
Generelt
Lad der være et system. Det har m ligninger og n ukendte rødder. Du kan skrive det sådan her:

Hovedmatrixen er kompileret ud fra systemets koefficienter. En kolonne med gratis medlemmer føjes til den udvidede matrix og adskilles af en bjælke for nemheds skyld.
Næste:
- den første række i matrixen ganges med koefficienten k=(-a21/a11);
- den første ændrede række og den anden række i matrixen tilføjes;
- i stedet for anden række indsættes resultatet af tilføjelsen fra det foregående afsnit i matrixen;
- nu er den første koefficient i den nye anden linje en11 × (-a21/a11) + a21 =-a21 + a21=0.
Nu udføres den samme serie af transformationer, kun den første og tredje linje er involveret. Følgelig erstattes elementet a21 i hvert trin i algoritmen med a31. Derefter gentages alt for a41, … am1. Resultatet er en matrix, hvor det første element i rækkerne [2, m] er lig nul. Nu skal du glemme alt om linje nummer et og udføre den samme algoritme fra den anden linje:
- k koefficient=(-a32/a22);
- den anden ændrede linje føjes til den "aktuelle" linje;
- resultatet af tilføjelsen erstattes af tredje, fjerde og så videre, mens den første og anden forbliver uændret;
- i rækkerne [3, m] i matricen er de to første elementer allerede lig med nul.
Algoritmen skal gentages, indtil koefficienten k=(-am, m-1/amm vises). Dette betyder, at algoritmen sidst blev kørt kun for den nederste ligning. Nu ligner matrixen en trekant eller har en trinformet form. Den nederste linje indeholder ligningen amn × x =bm. Koefficienten og frileddet er kendt, og roden udtrykkes gennem dem: x =bm/amn. Den resulterende rod sættes ind i den øverste række for at finde xn-1=(bm-1 - am-1, n×(bm/amn))÷am-1, n-1. Og så videre analogt: i hver næste linje er der en ny rod, og efter at have nået "toppen" af systemet, kan man finde et sæt løsninger [x1, … x ]. Det vil være den eneste.
Når der ikke er nogen løsninger
Hvis i en af matrixrækkerne alle elementer, bortset fra det frie led, er lig med nul, så ser ligningen svarende til denne række ud som 0=b. Det har ingen løsning. Og da en sådan ligning er inkluderet i systemet, så er løsningssættet for hele systemet tomt, det vil sige, det er degenereret.
Når der er et uendeligt antal løsninger
Det kan vise sig, at der i den reducerede trekantede matrix ikke er rækker med ét element - ligningens koefficient og et - et frit medlem. Der er kun strenge, der, når de bliver omskrevet, vil ligne en ligning med to eller flere variable. Det betyder, at systemet har et uendeligt antal løsninger. I dette tilfælde kan svaret gives i form af en generel løsning. Hvordan gør man det?
Allevariabler i matricen er opdelt i grundlæggende og frie. Grundlæggende - det er dem, der står "på kanten" af rækkerne i den trinvise matrix. Resten er gratis. I den generelle løsning er de grundlæggende variabler skrevet i form af de frie.
For nemheds skyld omskrives matrixen først tilbage til et ligningssystem. Så i den sidste af dem, hvor der kun var en grundlæggende variabel tilbage, forbliver den på den ene side, og alt andet overføres til den anden. Dette gøres for hver ligning med en grundvariabel. Så, i resten af ligningerne, hvor det er muligt, i stedet for grundvariablen, erstattes det opnåede udtryk for den. Hvis resultatet igen er et udtryk, der kun indeholder én grundvariabel, udtrykkes det derfra igen, og så videre, indtil hver grundvariabel er skrevet som et udtryk med frie variable. Dette er den generelle løsning af SLAE.
Du kan også finde den grundlæggende løsning af systemet - giv de frie variable alle værdier, og beregn derefter værdierne af de grundlæggende variabler for dette særlige tilfælde. Der er uendeligt mange særlige løsninger.
Løsning med specifikke eksempler
Her er et ligningssystem.
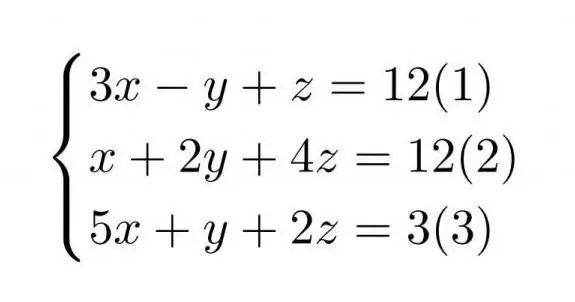
For nemheds skyld er det bedre at lave dens matrix med det samme
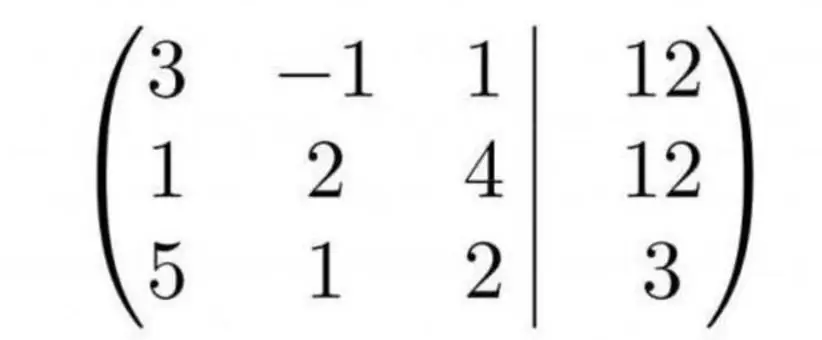
Det er kendt, at når man løser ved Gauss-metoden, vil ligningen svarende til den første række forblive uændret i slutningen af transformationerne. Derfor vil det være mere rentabelt, hvis det øverste venstre element i matrixen er det mindste - derefter de første elementerresten af rækkerne efter operationerne bliver nul. Det betyder, at det i den kompilerede matrix vil være fordelagtigt at sætte den anden række i stedet for den første.
Dernæst skal du ændre den anden og tredje linje, så de første elementer bliver nul. For at gøre dette skal du lægge dem til den første ganget med en koefficient:
anden linje: k=(-a21/a11)=(-3/1)=-3
a'21 =a21 + k×a11=3 + (-3))×1=0
a'22 =a22 + k×a12 =-1 + (- 3)×2=-7
a'23 =a23 + k×a13 =1+ (-3))×4=-11
b'2 =b2 + k×b1=12 + (-3))×12=-24
tredje linje: k=(-a31/a11)=(- 5/1)=-5
a'31 =a31+ k×a11=5 + (-5)×1=0
a'32 =a32+ k×a12 =1 + (-5)×2=-9
a'33 =a33 + k×a13 =2 + (-5)×4=-18
b'3=b3 + k×b1=3 + (-5))×12=-57
Nu, for ikke at blive forvirret, skal du skrive en matrix med mellemresultater af transformationer.
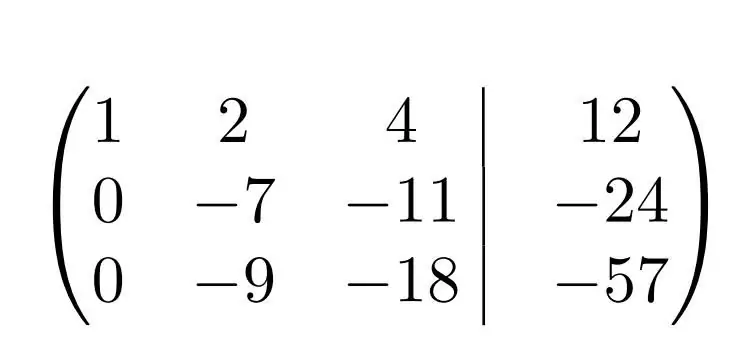
Det er klart, en sådan matrix kan gøres mere læsbar ved hjælp af nogle operationer. For eksempel kan du fjerne alle "minusser" fra den anden linje ved at gange hvert element med "-1".
Det er også værd at bemærke, at i den tredje linje er alle elementer multipla af tre. Så kan duklip strengen af med dette tal, multiplicer hvert element med "-1/3" (minus - på samme tid for at fjerne negative værdier).

Ser meget pænere ud. Nu skal vi lade den første linje være i fred og arbejde med den anden og tredje. Opgaven er at lægge den anden række til den tredje række ganget med en sådan faktor, at elementet a32 bliver nul.
k=(-a32/a22)=(-3/7)=-3/7 (hvis under nogle transformationer i svaret viste sig ikke at være et heltal, anbefales det at lade det være "som det er", i form af en almindelig brøk, og først derefter, når svarene modtages, beslutte, om du vil afrunde og konvertere til en anden form for notation)
a'32=a32 + k×a22=3 + (-3) /7)×7=3 + (-3)=0
a'33=a33 + k×a23=6 + (-3) /7)×11=-9/7
b'3 =b3 + k×b2=19 + (-3) /7)×24=-61/7
Matrixen skrives igen med nye værdier.
| 1 | 2 | 4 | 12 |
| 0 | 7 | 11 | 24 |
| 0 | 0 | -9/7 | -61/7 |
Som du kan se, har den resulterende matrix allerede en trinformet form. Derfor er yderligere transformationer af systemet ved Gauss-metoden ikke nødvendige. Det, der kan gøres her, er at fjerne den overordnede koefficient "-1/7" fra den tredje linje.

Nu alle sammenpæn. Pointen er lille - skriv matrixen igen i form af et ligningssystem og beregn rødderne
x + 2y + 4z=12 (1)
7y + 11z=24 (2)
9z=61 (3)
Algorithmen, hvormed rødderne nu vil blive fundet, kaldes det omvendte træk i Gauss-metoden. Ligning (3) indeholder værdien z:
z=61/9
Vend derefter tilbage til den anden ligning:
y=(24 - 11×(61/9))/7=-65/9
Og den første ligning giver dig mulighed for at finde x:
x=(12 - 4z - 2y)/1=12 - 4×(61/9) - 2×(-65/9)=-6/9=-2/3
Vi har ret til at kalde et sådant system fælles, og endda bestemt, det vil sige at have en unik løsning. Svaret er skrevet i følgende form:
x1=-2/3, y=-65/9, z=61/9.
Eksempel på et ubestemt system
Varianten af at løse et bestemt system ved Gauss-metoden er blevet analyseret, nu er det nødvendigt at overveje sagen, hvis systemet er ubestemt, det vil sige, der kan findes uendeligt mange løsninger til det.
x1 + x2 + x3 + x 4+ x5=7 (1)
3x1 + 2x2 + x3 + x 4 - 3x5=-2 (2)
x2 + 2x3 + 2x4 + 6x 5 =23 (3)
5x1 + 4x2 + 3x3 + 3x 4 - x5=12 (4)
Selve systemets form er allerede alarmerende, fordi antallet af ukendte er n=5, og rangeringen af systemmatricen er allerede nøjagtigt mindre end dette tal, fordi antallet af rækker er m=4, det vil sige den største rækkefølge af kvadratdeterminanten er 4. Så,Der er et uendeligt antal løsninger, og vi skal lede efter dens generelle form. Gauss-metoden til lineære ligninger giver dig mulighed for at gøre dette.
Først, som sædvanlig, kompileres den udvidede matrix.

Anden linje: koefficient k=(-a21/a11)=-3. I den tredje linje er det første element før transformationerne, så du behøver ikke røre ved noget, du skal lade det være som det er. Fjerde linje: k=(-a41/a11)=-5
Ved at gange elementerne i den første række med hver af deres koefficienter på skift og tilføje dem til de påkrævede rækker, får vi en matrix med følgende form:
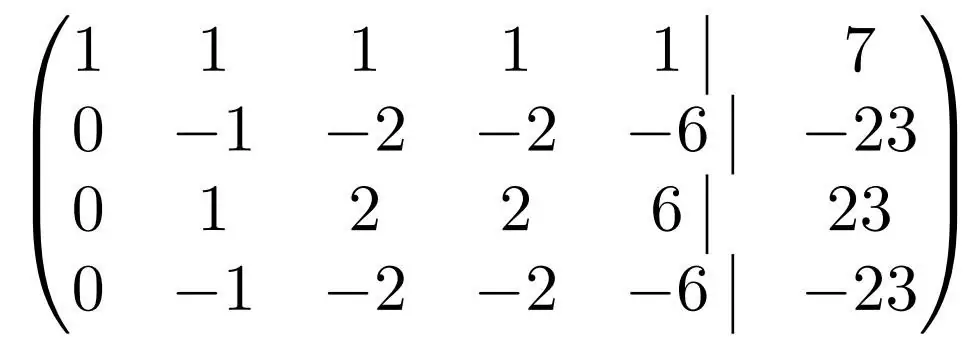
Som du kan se, består anden, tredje og fjerde række af elementer, der er proportionale med hinanden. Den anden og den fjerde er generelt ens, så en af dem kan fjernes med det samme, og resten ganges med koefficienten "-1" og få linje nummer 3. Og igen, lad en af to identiske linjer stå.
Resultatet er sådan en matrix. Systemet er endnu ikke nedskrevet, her er det nødvendigt at bestemme grundvariablene - stående ved koefficienterne a11=1 og a22=1, og gratis - alt det andet.
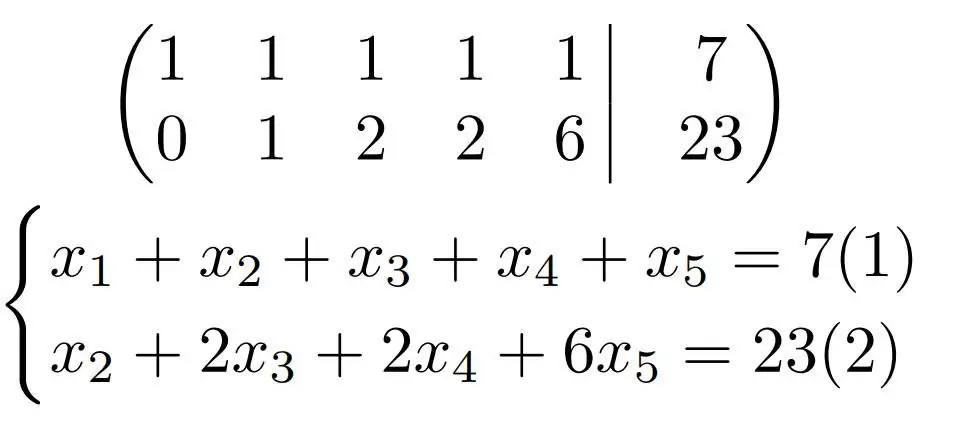
Der er kun én grundvariabel i den anden ligning - x2. Derfor kan det udtrykkes derfra ved at skrive gennem variablerne x3, x4, x5, som er gratis.
Erstat det resulterende udtryk i den første ligning.
Det viste sig en ligning, hvoriden eneste grundlæggende variabel er x1. Lad os gøre det samme med det som med x2.
Alle grundvariabler, som der er to af, er udtrykt som tre frie, nu kan du skrive svaret i generel form.
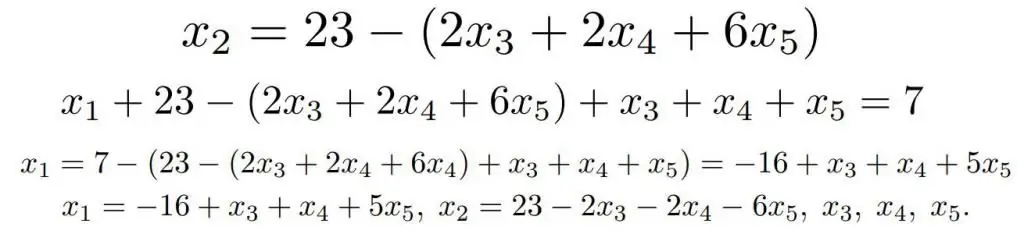
Du kan også angive en af systemets særlige løsninger. I sådanne tilfælde vælges som regel nuller som værdier for frie variable. Så vil svaret være:
-16, 23, 0, 0, 0.
Et eksempel på et inkonsekvent system
Løsning af inkonsistente ligningssystemer ved Gauss-metoden er den hurtigste. Den slutter, så snart der på et af stadierne opnås en ligning, der ikke har nogen løsning. Det vil sige, at stadiet med beregningen af rødderne, som er ret langt og trist, forsvinder. Følgende system er under overvejelse:
x + y - z=0 (1)
2x - y - z=-2 (2)
4x + y - 3z=5 (3)
Som sædvanligt er matrix kompileret:
| 1 | 1 | -1 | 0 |
| 2 | -1 | -1 | -2 |
| 4 | 1 | -3 | 5 |
Og reduceret til en trinvis form:
k1 =-2k2 =-4
| 1 | 1 | -1 | 0 |
| 0 | -3 | 1 | -2 |
| 0 | 0 | 0 | 7 |
Efter den første transformation indeholder den tredje linje en ligning med formen
0=7, ingen løsning. Derfor systemeter inkonsekvent, og svaret er det tomme sæt.
Fordele og ulemper ved metoden
Hvis du vælger, hvilken metode du vil løse SLAE på papir med en pen, så ser den metode, der blev overvejet i denne artikel, den mest attraktive ud. I elementære transformationer er det meget sværere at blive forvirret, end det sker, hvis du manuelt skal lede efter determinanten eller en eller anden vanskelig invers matrix. Men hvis du bruger programmer til at arbejde med data af denne type, for eksempel regneark, så viser det sig, at sådanne programmer allerede indeholder algoritmer til beregning af hovedparametrene for matricer - determinanten, minor, inverse og transponerede matricer og så videre. Og hvis du er sikker på, at maskinen selv vil beregne disse værdier og ikke begår en fejl, er det mere hensigtsmæssigt at bruge matrixmetoden eller Cramers formler, fordi deres anvendelse begynder og slutter med beregningen af determinanter og inverse matricer.
Application
Da den Gaussiske løsning er en algoritme, og matrixen i virkeligheden er en todimensional matrix, kan den bruges i programmering. Men da artiklen placerer sig som en guide "for dummies", skal det siges, at det nemmeste sted at sætte metoden ind er regneark, for eksempel Excel. Igen vil enhver SLAE, der er indtastet i en tabel i form af en matrix, blive betragtet af Excel som en todimensionel matrix. Og til operationer med dem er der mange gode kommandoer: addition (du kan kun tilføje matricer af samme størrelse!), Multiplikation med et tal, matrixmultiplikation (også medvisse restriktioner), finde de inverse og transponerede matricer og, vigtigst af alt, beregning af determinanten. Hvis denne tidskrævende opgave erstattes af en enkelt kommando, er det meget hurtigere at bestemme rangeringen af en matrix og derfor fastslå dens kompatibilitet eller inkonsistens.






