Pyramid sammen med et prisme er et perfekt polyeder i tredimensionelt rum, deres geometriske karakteristika studeres i gymnasiet. I denne artikel vil vi overveje, hvad pyramider er, hvilke elementer de består af, og også kort karakterisere de korrekte pyramider.
Geometrisk figurpyramide
Fra et geometrisk synspunkt er pyramiden en rumlig figur, der består af en polygon og flere trekanter. At få denne figur er ret enkel. For at gøre dette skal du tage en polygon med n sider, derefter vælge et vilkårligt punkt i rummet, der ikke vil ligge i polygonens plan, og forbinde hvert hjørne af polygonen til dette punkt. Det er klart, at figuren, der er dannet på denne måde, vil have n trekanter forbundet med hinanden i et toppunkt.
For at visualisere den geometriske form af den beskrevne figur, lad os tage et billede.

Dette viser en firkantet pyramide, hvis basis erfirkant, og sidefladen er dannet af fire trekanter, der har et fælles toppunkt.
Pyramideelementer
Som ethvert polyeder er pyramiden dannet af tre typer elementer:
- kanter;
- tops;
- ribs.
Ansigter er dele af planer, der adskiller en figurs indre volumen fra det omgivende rum. Hvis bunden af pyramiden indeholder en n-gon, så er antallet af dens flader altid n+1. Af disse er n sider trekantede, og den ene side er den nævnte n-gonale base.
Handpunkter er punkter, hvor tre eller flere flader af en figur skærer hinanden. Basisområdet indeholder n hjørner, som hver er dannet af to trekantede flader og en base. Punktet, hvor n trekantede sider mødes, kaldes toppen af pyramiden. Den betragtede figur består således af n+1 hjørner.
Kanter er lige linjer, der vises, når to flader skærer hinanden. Hver kant er afgrænset af to spidser i dens ender. Enhver pyramide med en n-gon base indeholder 2n kanter. Halvdelen af dette tal, det vil sige n, dannes udelukkende af skæringspunktet mellem sidetrekanter.
Mulige typer figurer
Navnet på den betragtede figur er entydigt bestemt af typen af polygon ved bunden. Hvis den f.eks. har tre hjørner og tre sider, vil pyramiden være trekantet, hvis fire - firkantet, og så videre.
Polygon kan være konveks og konkav, såvel som almindelig og generel type. Alt dette bestemmer også pyramidens udseende.
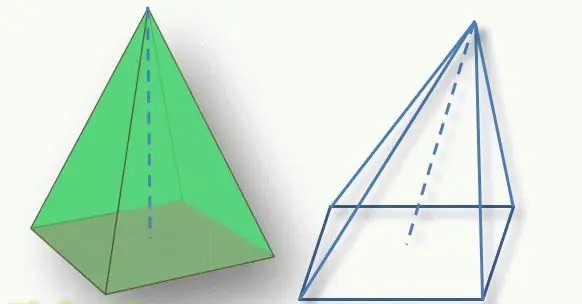
Et vigtigt punkt ved bestemmelse af figurtypen er placeringen af toppen af pyramiden i forhold til dens base. Det vinkelrette segment tegnet fra toppen til den polygonale base kaldes figurens højde. Hvis dette segment skærer basen i dets geometriske centrum (for en trekant er dette skæringspunktet mellem medianer, for en firkant skæringspunktet mellem diagonaler), så kaldes figuren en ret linje. Ellers taler de om en skrå pyramide.
Hvis basens n-gon er regulær (ligesidet trekant, firkant osv.), og figuren er lige, så kaldes den en regulær pyramide.
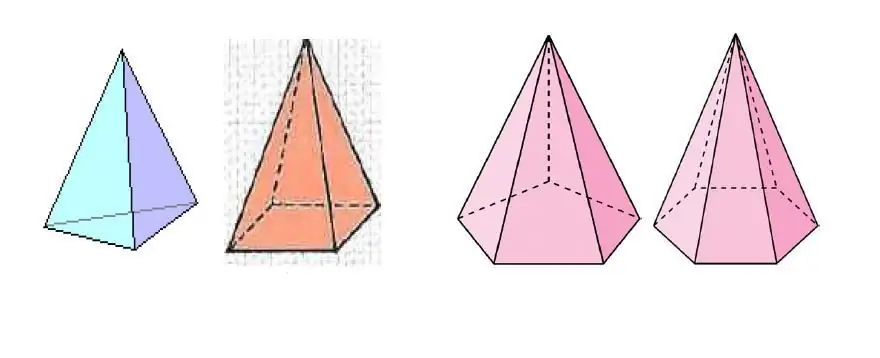
Billedet ovenfor viser flere pyramider, som adskiller sig i antallet af sider af polygonen ved bunden.
egenskaber ved almindelige pyramider
Disse pyramider adskiller sig fra andre figurer i denne klasse ved en høj grad af symmetri. I denne forbindelse er det praktisk at udføre forskellige geometriske beregninger med dem, for eksempel volumen eller overfladeareal.
En regulær pyramide indeholder en n-gon ved sin base, hvis areal er unikt bestemt ud fra viden om længden af dens side. Figurens sideflade er dannet af n identiske trekanter, som er ligesidede. Kanterne af en almindelig pyramide placeret på den laterale overflade er lig med hinanden. Værdien af længden af denne kant bruges ofte, når man beregner en figurs apotem og bestemmer overfladearealet.
Højden af en regulær pyramide er den anden vigtige egenskab ved figuren (den første er længden af kantengrunde). Højde bruges ved beregning af volumen.
Ethvert plan parallelt med bunden, som skærer pyramidens sideflader, fører til dannelsen af et polygon alt snit. Det er homotetisk med hensyn til basispolygonen. Den beskrevne skiveoperation fører til dannelsen af en hel klasse af nye figurer - afkortede regulære pyramider.
De mest berømte pyramider

Selvfølgelig er disse de regulære firkantede pyramider af de egyptiske faraoer. På et sted kaldet Giza er der mere end 100 af disse stenmonumenter, perfektion af design og nøjagtigheden af de geometriske parametre, som fortsætter med at forbløffe videnskabsmænd den dag i dag. Den største af dem er Keops-pyramiden, som er omkring 146 meter høj og omkring 230 meter lang.
Hvad præcis disse pyramider tjente til, samt hvilke mekanismer og hvornår de blev bygget, ved ingen den dag i dag.






