Der er objekter, der er i stand til at ændre tætheden af den elektromagnetiske strålingsflux, der falder på dem, det vil sige enten at øge den ved at samle den på et tidspunkt eller mindske den ved at sprede den. Disse objekter kaldes linser i fysik. Lad os se nærmere på dette problem.
Hvad er linser i fysik?
Dette koncept betyder absolut ethvert objekt, der er i stand til at ændre udbredelsesretningen for elektromagnetisk stråling. Dette er den generelle definition af linser i fysik, som omfatter optiske briller, magnetiske og gravitationslinser.
I denne artikel vil fokus være på optiske briller, som er genstande lavet af et gennemsigtigt materiale og begrænset af to overflader. En af disse overflader skal nødvendigvis have krumning (det vil sige være en del af en kugle med begrænset radius), ellers vil objektet ikke have den egenskab, at det ændrer lysstrålernes udbredelsesretning.
Linsens princip

essensen af arbejdet med dette ukompliceredeoptisk objekt er fænomenet brydning af solens stråler. I begyndelsen af det 17. århundrede offentliggjorde den berømte hollandske fysiker og astronom Willebrord Snell van Rooyen loven om brydning, som i øjeblikket bærer hans efternavn. Formuleringen af denne lov er som følger: når sollys passerer gennem grænsefladen mellem to optisk transparente medier, så er produktet af sinusen af indfaldsvinklen mellem strålen og normalen til overfladen og brydningsindekset for mediet, hvori den forplanter sig er en konstant værdi.

For at præcisere ovenstående, lad os give et eksempel: lad lyset falde på vandoverfladen, mens vinklen mellem normalen til overfladen og strålen er θ1. Derefter brydes lysstrålen og begynder sin udbredelse i vandet allerede i en vinkel θ2 til normalen til overfladen. Ifølge Snells lov får vi: sin(θ1)n1=synd(θ2) n2, hvor n1 og n2 er brydningsindekserne for luft og vand, henholdsvis. Hvad er brydningsindekset? Dette er en værdi, der viser, hvor mange gange udbredelseshastigheden af elektromagnetiske bølger i vakuum er større end for et optisk transparent medium, dvs. n=c/v, hvor c og v er lysets hastigheder i vakuum og i henholdsvis medium.
Fysikken i tilsynekomsten af brydning ligger i implementeringen af Fermats princip, ifølge hvilket lys bevæger sig på en sådan måde, at det overvinder afstanden fra et punkt til et andet i rummet på kortest tid.
Linsetyper

Typen af optisk linse i fysik bestemmes udelukkende af formen på de overflader, der danner den. Retningen af brydningen af strålen, der falder ind på dem, afhænger af denne form. Så hvis krumningen af overfladen er positiv (konveks), vil lysstrålen, når den forlader linsen, forplante sig tættere på sin optiske akse (se nedenfor). Omvendt, hvis krumningen af overfladen er negativ (konkav), og derefter passerer gennem det optiske glas, vil strålen bevæge sig væk fra sin centrale akse.
Bemærk igen, at en overflade med en hvilken som helst krumning bryder stråler på samme måde (i henhold til Stellas lov), men normalerne til dem har en anden hældning i forhold til den optiske akse, hvilket resulterer i forskellig opførsel af den brydte stråle.
En linse afgrænset af to konvekse overflader kaldes en konvergerende linse. Til gengæld, hvis det er dannet af to overflader med negativ krumning, kaldes det spredning. Alle andre typer optiske briller er forbundet med en kombination af disse overflader, hvortil der også er tilføjet et plan. Hvilken egenskab den kombinerede linse vil have (divergent eller konvergerende) afhænger af den samlede krumning af radierne af dens overflader.
Linseelementer og stråleegenskaber

For at indbygge linser i billedfysik skal du stifte bekendtskab med elementerne i dette objekt. De er anført nedenfor:
- Optisk hovedakse og center. I det første tilfælde betyder de en lige linje, der går vinkelret på linsen gennem dens optiske centrum. Sidstnævnte er til gengæld et punkt inde i linsen, der går igennem hvilket strålen ikke oplever brydning.
- Brændvidde og fokus - afstanden mellem midten og et punkt på den optiske akse, som samler alle de stråler, der falder ind på linsen parallelt med denne akse. Denne definition gælder for indsamling af optiske briller. I tilfælde af divergerende linser er det ikke selve strålerne, der vil konvergere til et punkt, men deres imaginære fortsættelse. Dette punkt kaldes hovedfokus.
- Optisk effekt. Dette er navnet på den gensidige af brændvidden, det vil sige D \u003d 1 / f. Det måles i dioptrier (dioptrier), det vil sige 1 dioptri.=1 m-1.
Følgende er hovedegenskaberne for de stråler, der passerer gennem linsen:
- stråle, der passerer gennem det optiske center, ændrer ikke dens bevægelsesretning;
- stråler, der falder parallelt med den optiske hovedakse, ændrer deres retning, så de passerer gennem hovedfokuset;
- stråler, der falder på optisk glas i enhver vinkel, men passerer gennem dets fokus, ændrer deres udbredelsesretning på en sådan måde, at de bliver parallelle med den optiske hovedakse.
Ovenstående egenskaber af stråler for tynde linser i fysik (som de kaldes, fordi uanset hvilke kugler de dannes, og hvor tykke de er, er det kun objektets optiske egenskaber), der bruges til at bygge billeder i dem.
Billeder i optiske briller: hvordan bygger man?
Nedenfor er en figur, der beskriver skemaerne til at konstruere billeder i de konvekse og konkave linser af et objekt(rød pil) afhængig af dens position.
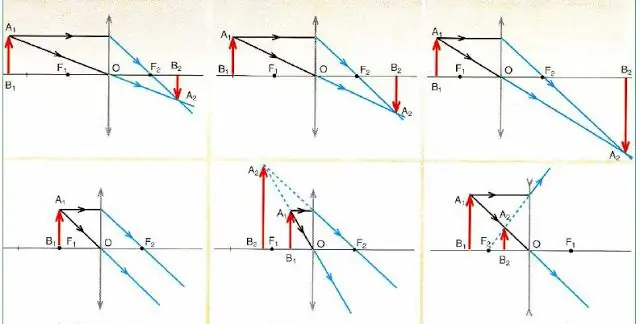
Vigtige konklusioner følger af analysen af kredsløbene i figuren:
- Ethvert billede er bygget på kun 2 stråler (passerer gennem midten og parallelt med den optiske hovedakse).
- Konvergerende linser (angivet med pile i enderne pegende udad) kan give både et forstørret og formindsket billede, som igen kan være ægte (ægte) eller imaginære.
- Hvis objektet er i fokus, danner linsen ikke sit billede (se det nederste diagram til venstre i figuren).
- Spredning af optiske briller (angivet med pile i enderne, der peger indad) giver altid et reduceret og virtuelt billede uanset objektets position.
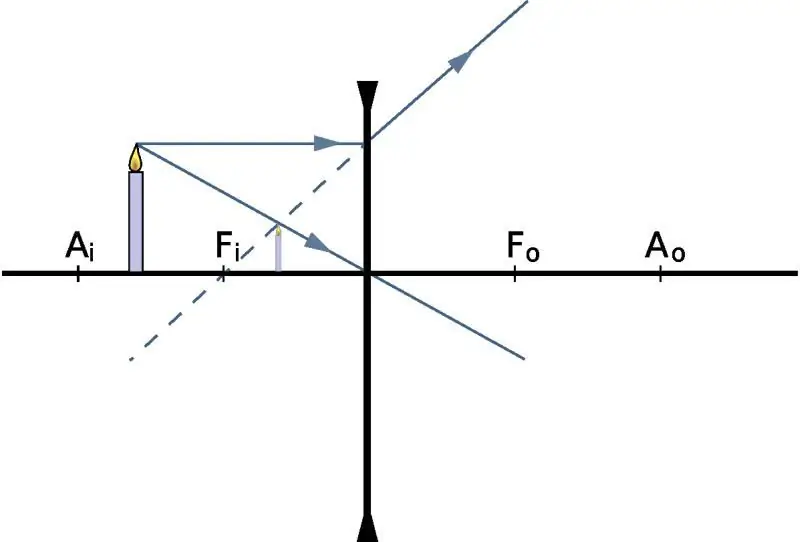
Find afstanden til et billede
For at bestemme, i hvilken afstand billedet vil blive vist, ved at kende selve objektets position, giver vi linseformlen i fysik: 1/f=1/do + 1 /d i, hvor do og di er afstanden til objektet og til dets billede fra det optiske center, henholdsvis f er hovedfokus. Hvis vi taler om et samlende optisk glas, så vil f-tallet være positivt. Omvendt, for en divergerende linse er f negativ.
Lad os bruge denne formel og løse et simpelt problem: Lad objektet være i en afstand do=2f fra midten af det optiske glas. Hvor vises hans billede?
Fra problemets tilstand har vi: 1/f=1/(2f)+1/di. Fra: 1/di=1/f - 1/(2f)=1/(2f), dvs. di=2 f. Billedet vil således fremstå i en afstand af to brændpunkter fra linsen, men på den anden side end selve objektet (dette er angivet med det positive fortegn for værdien di).
En kort historie
Det er nysgerrigt at give ordet "linse" etymologien. Det kommer fra de latinske ord lens og lentis, som betyder "linse", da optiske genstande i deres form virkelig ligner frugten af denne plante.
Brydningskraften af sfæriske gennemsigtige legemer var kendt af de gamle romere. Til dette formål brugte de runde glasbeholdere fyldt med vand. Selve glaslinser begyndte først at blive fremstillet i det 13. århundrede i Europa. De blev brugt som læseredskab (moderne briller eller forstørrelsesglas).
Den aktive brug af optiske objekter i fremstillingen af teleskoper og mikroskoper går tilbage til det 17. århundrede (i begyndelsen af dette århundrede opfandt Galileo det første teleskop). Bemærk, at den matematiske formulering af Stellas brydningslov, uden viden om hvilken det er umuligt at fremstille linser med ønskede egenskaber, blev udgivet af en hollandsk videnskabsmand i begyndelsen af det samme 17. århundrede.
Andre linser
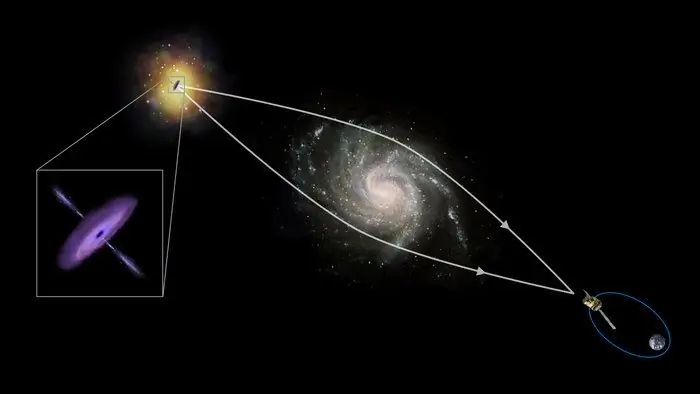
Som nævnt ovenfor er der ud over optiske brydningsobjekter også magnetiske og gravitationsobjekter. Et eksempel på førstnævnte er magnetiske linser i et elektronmikroskop, et levende eksempel på sidstnævnte er forvrængning af retningen af lysstrømmen,når den passerer i nærheden af massive rumlegemer (stjerner, planeter).






