Opløsning er et billeddannelsessystems evne til at gengive detaljerne i et objekt og afhænger af faktorer såsom den anvendte belysningstype, sensorens pixelstørrelse og optikkens muligheder. Jo mindre detalje af motivet er, jo højere er objektivets krævede opløsning.
Introduktion til løsningsprocessen
Billedkvaliteten af kameraet afhænger af sensoren. Kort sagt er en digital billedsensor en chip inde i et kamerahus, der indeholder millioner af lysfølsomme pletter. Størrelsen af et kameras sensor bestemmer, hvor meget lys der kan bruges til at skabe et billede. Jo større sensoren er, desto bedre billedkvalitet, da der indsamles mere information. Typisk annoncerer digitale kameraer på markedet efter sensorstørrelser på 16 mm, Super 35 mm og nogle gange op til 65 mm.
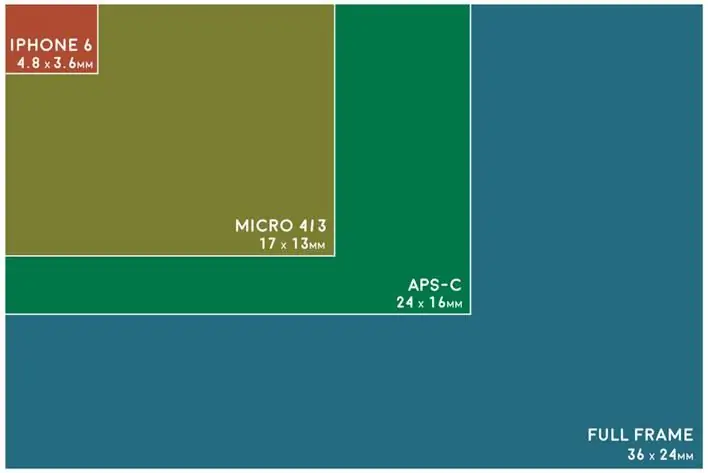
Når størrelsen af sensoren øges, vil dybdeskarpheden falde ved en given blænde, da en større modpart kræver, at du kommer tættere påobjekt eller brug en længere brændvidde til at udfylde rammen. For at bevare den samme dybdeskarphed skal fotografen bruge mindre blændeåbninger.
Denne lave dybdeskarphed kan være ønskelig, især for at opnå baggrundssløring til portrætter, men landskabsfotografering kræver mere dybde, hvilket er lettere at fange med den fleksible blændestørrelse på kompaktkameraer.
Opdeling af antallet af vandrette eller lodrette pixels på en sensor vil indikere, hvor meget plads hver enkelt optager på et objekt, og kan bruges til at evaluere linsens løsningsevne og løse kunders bekymringer om enhedens digitale billedpixelstørrelse. Som udgangspunkt er det vigtigt at forstå, hvad der faktisk kan begrænse systemets opløsning.
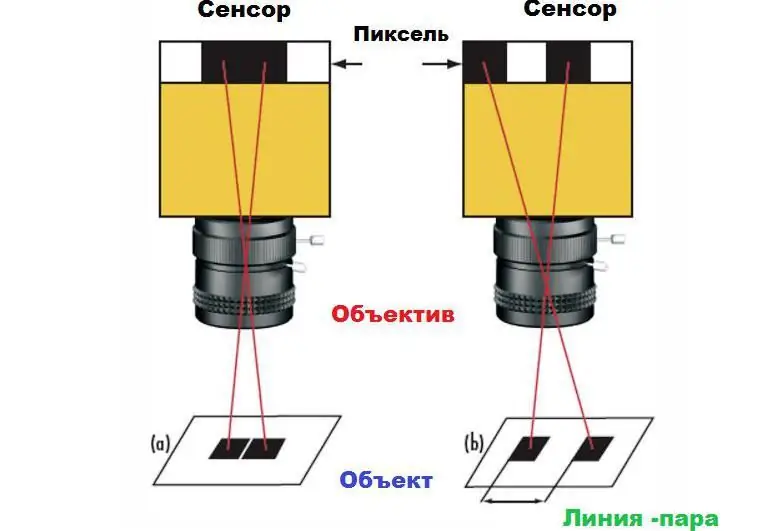
Dette udsagn kan demonstreres med eksemplet med et par firkanter på en hvid baggrund. Hvis firkanterne på kamerasensoren er afbildet til nabopixel, vil de fremstå som ét stort rektangel i billedet (1a) i stedet for to separate firkanter (1b). For at skelne mellem firkanterne kræves der et vist mellemrum mellem dem, mindst én pixel. Denne minimumsafstand er systemets maksimale opløsning. Den absolutte grænse bestemmes af størrelsen af pixels på sensoren samt deres antal.
Målelinsens karakteristika
Forholdet mellem vekslende sorte og hvide firkanter beskrives som et lineært par. Typisk bestemmes opløsningen af frekvensen,målt i linjepar pr. millimeter - lp/mm. Desværre er objektivopløsning i cm ikke et absolut tal. Ved en given opløsning vil evnen til at se de to firkanter som separate objekter afhænge af gråskalaniveauet. Jo større gråskalaadskillelse der er mellem dem og rummet, jo mere stabil er evnen til at løse disse firkanter. Denne opdeling af gråskalaen er kendt som frekvenskontrast.
Den rumlige frekvens er angivet i lp/mm. Af denne grund er det ekstremt nyttigt at beregne opløsning i form af lp/mm, når man sammenligner objektiver og bestemmer det bedste valg for givne sensorer og applikationer. Den første er, hvor systemopløsningsberegningen starter. Startende med sensoren er det lettere at bestemme, hvilke linsespecifikationer der er nødvendige for at opfylde kravene til enheden eller andre applikationer. Den højeste frekvens, som sensoren, Nyquist, tillader, er faktisk to pixels eller et linjepar.
Definitionslinseopløsning, også kaldet systembilledopløsning, kan bestemmes ved at gange størrelsen i Μm med 2 for at skabe et par og dividere med 1000 for at konvertere til mm:
lp/mm=1000/ (2 X pixel)
Sensorer med større pixels vil have lavere opløsningsgrænser. Sensorer med mindre pixels vil yde bedre i henhold til linseopløsningsformlen ovenfor.
Aktivt sensorområde
Du kan beregne den maksimale opløsning for objektetvisning. For at gøre dette er det nødvendigt at skelne mellem indikatorer som forholdet mellem størrelsen af sensoren, synsfeltet og antallet af pixels på sensoren. Størrelsen af sidstnævnte refererer til parametrene for kamerasensorens aktive område, norm alt bestemt af størrelsen på dets format.
De nøjagtige proportioner vil dog variere efter billedformat, og nominelle sensorstørrelser bør kun bruges som en rettesnor, især for telecentriske objektiver og høje forstørrelser. Sensorstørrelsen kan beregnes direkte ud fra pixelstørrelsen og det aktive antal pixels for at udføre objektivopløsningstest.
Tabellen viser Nyquist-grænsen forbundet med pixelstørrelser fundet på nogle meget almindeligt brugte sensorer.
| Pixelstørrelse (µm) | Koblet Nyquist-grænse (lp/mm) |
| 1, 67 | 299, 4 |
| 2, 2 | 227, 3 |
| 3, 45 | 144, 9 |
| 4, 54 | 110, 1 |
| 5, 5 | 90, 9 |
Når pixelstørrelserne falder, stiger den tilhørende Nyquist-grænse i lp/mm proportion alt. For at bestemme den absolutte mindste opløselige plet, der kan ses på et objekt, skal forholdet mellem synsfeltet og størrelsen af sensoren beregnes. Dette er også kendt som primær augmentation.(PMAG)-systemer.
Forholdet forbundet med systemet PMAG gør det muligt at skalere billedrummets opløsning. Når man designer en applikation, er den typisk ikke angivet i lp/mm, men snarere i mikron (µm) eller fraktioner af en tomme. Du kan hurtigt hoppe til den ultimative opløsning af et objekt ved at bruge formlen ovenfor for at gøre det nemmere at vælge objektivopløsningen z. Det er også vigtigt at huske på, at der er mange yderligere faktorer, og ovenstående begrænsning er meget mindre udsat for fejl end kompleksiteten i at tage højde for mange faktorer og beregne dem ved hjælp af ligninger.
Beregn brændvidde
Opløsningen af et billede er antallet af pixels i det. Designet i to dimensioner, for eksempel 640X480. Beregninger kan udføres separat for hver dimension, men for nemheds skyld reduceres dette ofte til én. For at foretage nøjagtige målinger på et billede skal du bruge minimum to pixels for hvert mindste område, du vil detektere. Størrelsen af sensoren refererer til en fysisk indikator og er som regel ikke angivet i pasdataene. Den bedste måde at bestemme størrelsen på en sensor på er at se på pixelparametrene på den og gange dem med billedformatet, i hvilket tilfælde objektivets opløsningsevne løser problemerne med et dårligt billede.
F.eks. har Basler acA1300-30um-kameraet en pixelstørrelse på 3,75 x 3,75um og en opløsning på 1296 x 966 pixels. Sensorstørrelsen er 3,75 µm x 1296 x 3,75 µm x 966=4,86 x 3,62 mm.
Sensorformat henviser til den fysiske størrelse og afhænger ikke af pixelstørrelsen. Denne indstilling bruges tilbestemme hvilket objektiv kameraet er kompatibelt med. For at de kan matche, skal objektivformatet være større end eller lig med sensorstørrelsen. Hvis der bruges et objektiv med et mindre billedformat, vil billedet opleve vignettering. Dette får områder af sensoren uden for kanten af objektivformatet til at blive mørke.
Pixels og kameravalg

For at se objekterne på billedet skal der være nok mellemrum mellem dem, så de ikke smelter sammen med nabopixel, ellers vil de ikke kunne skelnes fra hinanden. Hvis objekterne er en pixel hver, skal adskillelsen mellem dem også være mindst et element, det er takket være dette, at der dannes et par linjer, som faktisk har to pixels i størrelse. Dette er en af grundene til, at det er forkert at måle opløsningen på kameraer og objektiver i megapixel.
Det er faktisk nemmere at beskrive et systems opløsningsevne i form af linjeparfrekvens. Det følger heraf, at når pixelstørrelsen falder, øges opløsningen, fordi du kan placere mindre objekter på mindre digitale elementer, have mindre mellemrum mellem dem og stadig opløse afstanden mellem de motiver, du optager.
Dette er en forenklet model af, hvordan kameraets sensor registrerer objekter uden at tage hensyn til støj eller andre parametre, og det er den ideelle situation.
MTF-kontrastdiagrammer
De fleste linser er ikke perfekte optiske systemer. Lys, der passerer gennem en linse, gennemgår en vis grad af nedbrydning. Spørgsmålet er, hvordan man vurderer dettenedbrydning? Før du besvarer dette spørgsmål, er det nødvendigt at definere begrebet "modulation". Sidstnævnte er et mål for kontrasten len ved en given frekvens. Man kunne prøve at analysere billeder fra den virkelige verden taget gennem en linse for at bestemme modulering eller kontrast for detaljer af forskellige størrelser eller frekvenser (mellemrum), men dette er meget upraktisk.
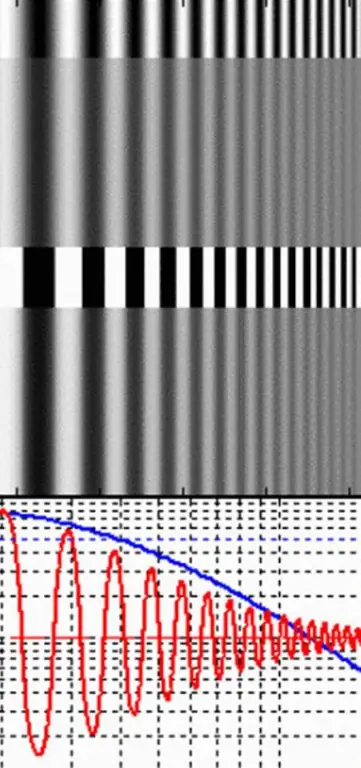
I stedet er det meget nemmere at måle modulering eller kontrast for par af alternerende hvide og mørke linjer. De kaldes rektangulært gitter. Intervallet af linjer i et rektangulært bølgegitter er frekvensen (v), for hvilken linsens modulations- eller kontrastfunktion og opløsningen måles i cm.
Den maksimale mængde lys kommer fra de lyse bånd og minimum fra de mørke bånd. Hvis lys måles i lysstyrke (L), kan moduleringen bestemmes i henhold til følgende ligning:
modulation=(Lmax - Lmin) / (Lmax + Lmin), hvor: Lmax er den maksimale lysstyrke af hvide linjer i gitteret, og Lmin er minimumslysstyrken for mørke.
Når modulering defineres ud fra lys, omtales det ofte som Michelson-kontrast, fordi det tager forholdet mellem luminans fra lyse og mørke bånd for at måle kontrast.
Der er for eksempel et firkantbølgegitter med en bestemt frekvens (v) og modulering, og en iboende kontrast mellem mørke og lyse områder reflekteret fra dette gitter gennem linsen. Billedmodulation og dermed objektivkontrast måles for en given frekvenstakter (v).
Modulationsoverførselsfunktionen (MTF) er defineret som moduleringen M i af billedet divideret med moduleringen af stimulus (objekt) M o, som vist i den følgende ligning.
|
MTF (v)=M i / M 0 |
USF-testgitter er trykt på 98 % klart laserpapir. Sort laserprintertoner har en reflektans på omkring 10%. Så værdien for M 0 er 88 %. Men da film har et mere begrænset dynamisk område sammenlignet med det menneskelige øje, er det sikkert at antage, at M 0 i det væsentlige er 100 % eller 1. Så ovenstående formel koger mere ned til følgende mere simpel ligning:
|
MTF (v)=Mi |
Så MTF-lensen for en given gitterfrekvens (v) er simpelthen den målte gittermodulation (Mi), når den fotograferes gennem en linse på film.
Mikroskopopløsning
Opløsningen af et mikroskopobjektiv er den korteste afstand mellem to forskellige punkter i okularets synsfelt, der stadig kan skelnes som forskellige objekter.
Hvis to punkter er tættere på hinanden end din opløsning, vil de virke slørede, og deres positioner vil være unøjagtige. Mikroskopet kan tilbyde høj forstørrelse, men hvis linserne er af dårlig kvalitet, vil den resulterende dårlige opløsning forringe billedkvaliteten.
Nedenfor er Abbe-ligningen, hvor opløsningenstyrken af et mikroskopobjektiv z er opløsningsevnen lig med bølgelængden af det anvendte lys divideret med 2 (objektivets numeriske blænde).
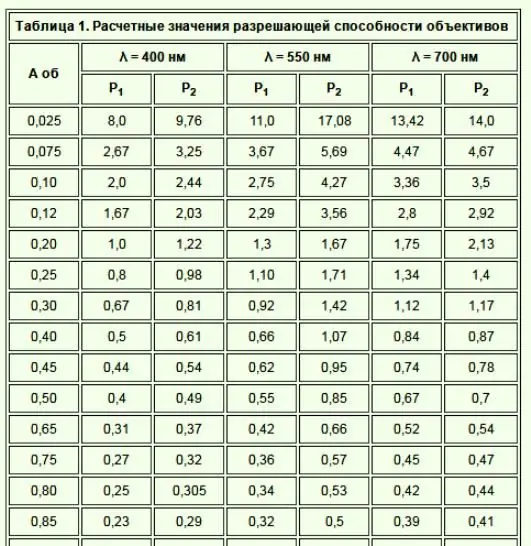
Flere elementer påvirker opløsningen af et mikroskop. Et optisk mikroskop indstillet til høj forstørrelse kan producere et billede, der er sløret, men det har stadig objektivets maksimale opløsning.
Den digitale blænde på et objektiv påvirker opløsningen. Opløsningsevnen for et mikroskopobjektiv er et tal, der angiver en linses evne til at opsamle lys og opløse et punkt i en fast afstand fra objektivet. Det mindste punkt, der kan opløses af linsen, er proportional med bølgelængden af det opsamlede lys divideret med det numeriske blændetal. Derfor svarer et større tal til en større evne hos objektivet til at registrere et fremragende punkt i synsfeltet.. Linsens numeriske blænde afhænger også af mængden af optisk aberrationskorrektion.
Opløsning af teleskoplinsen
Som en lystragt er et teleskop i stand til at opsamle lys i forhold til arealet af hullet, denne egenskab er hovedlinsen.
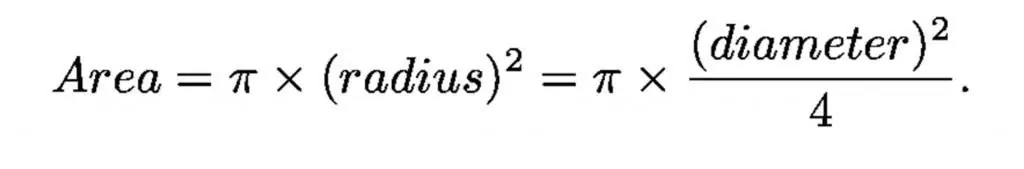
Diameteren af den mørke tilpassede pupil i det menneskelige øje er lige under 1 centimeter, og diameteren af det største optiske teleskop er 1.000 centimeter (10 meter), så det største teleskop er en million gange større i samlingen område end det menneskelige øje.

Det er grunden til, at teleskoper ser svagere genstande end mennesker. Og har enheder, der akkumulerer lys ved hjælp af elektroniske detekteringssensorer i mange timer.
Der er to hovedtyper af teleskoper: linsebaserede refraktorer og spejlbaserede reflektorer. Store teleskoper er reflektorer, fordi spejle ikke behøver at være gennemsigtige. Teleskopspejle er blandt de mest præcise designs. Den tilladte fejl på overfladen er omkring 1/1000 af bredden af et menneskehår - gennem et 10 meter hul.
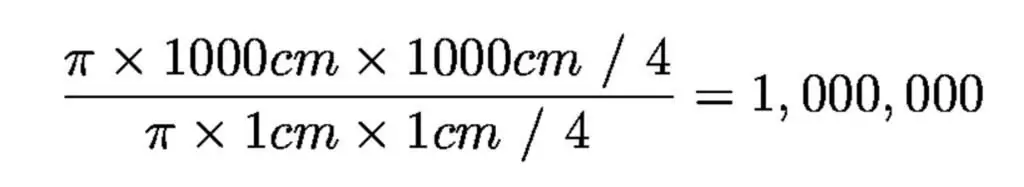
Spejle plejede at være lavet af enorme tykke glasplader for at forhindre dem i at falde. Nutidens spejle er tynde og fleksible, men er computerstyret eller på anden måde segmenteret og justeret ved computerstyring. Udover opgaven med at finde svage genstande, er astronomens mål også at se deres fine detaljer. Den grad, i hvilken detaljer kan genkendes, kaldes opløsning:
- Fuzzy billeder=dårlig opløsning.
- Klare billeder=god opløsning.
På grund af lysets bølgenatur og fænomener kaldet diffraktion, begrænser diameteren af et teleskops spejl eller linse dets ultimative opløsning i forhold til teleskopets diameter. Opløsningen betyder her den mindste kantede detalje, der kan genkendes. Små værdier svarer til fremragende billeddetaljer.
Radioteleskoper skal være meget store for at give god opløsning. Jordens atmosfære erturbulente og slørede teleskopbilleder. Terrestriske astronomer kan sjældent nå den maksimale opløsning af apparatet. Atmosfærens turbulente effekt på en stjerne kaldes syn. Denne turbulens får stjernerne til at "glitre". For at undgå disse atmosfæriske sløringer sender astronomer teleskoper ud i rummet eller placerer dem på høje bjerge med stabile atmosfæriske forhold.
Eksempler på parameterberegning
Data til bestemmelse af Canon-objektivopløsning:
- Pixelstørrelse=3,45 µm x 3,45 µm.
- Pixels (H x V)=2448 x 2050.
- Ønsket synsfelt (vandret)=100 mm.
- Sensoropløsningsgrænse: 1000/2x3, 45=145 lp/mm.
- Sensordimensioner:3,45x2448/1000=8,45 mm3, 45x2050/1000=7,07 mm.
- PMAG:8, 45/100=0,0845 mm.
- Måleobjektivopløsning: 145 x 0,0845=12,25 lp/mm.
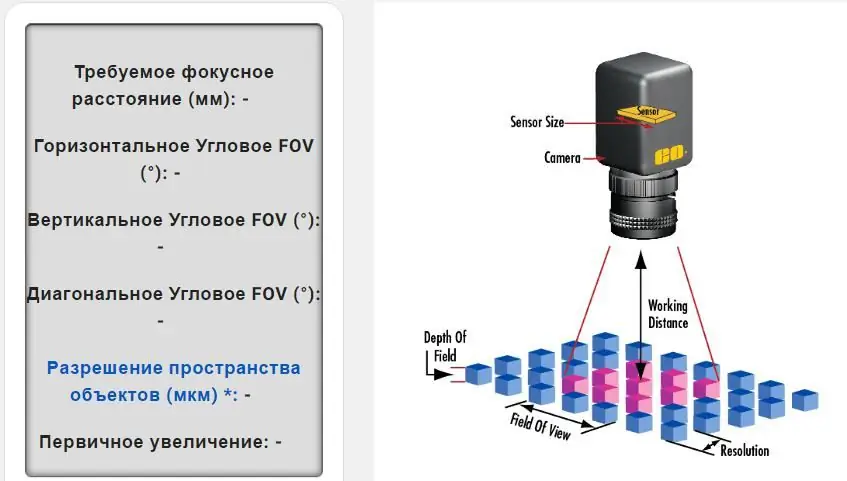
Faktisk er disse beregninger ret komplekse, men de vil hjælpe dig med at skabe et billede baseret på sensorstørrelse, pixelformat, arbejdsafstand og synsfelt i mm. Beregning af disse værdier vil bestemme den bedste linse til dine billeder og applikation.
Problemer med moderne optik

Desværre skaber en fordobling af størrelsen af sensoren yderligere problemer for objektiver. En af de vigtigste parametre, der påvirker prisen på et billedobjektiv, er formatet. At designe et objektiv til en sensor i større format krævertalrige individuelle optiske komponenter, som burde være større og overførslen af systemet mere stiv.
Et objektiv designet til en 1"-sensor kan koste fem gange så meget som et objektiv designet til en ½"-sensor, selvom det ikke kan bruge de samme specifikationer med begrænset pixelopløsning. Omkostningskomponenten skal overvejes, før hvordan for at bestemme opløsningsevnen for en linse.
Optisk billedbehandling står i dag over for flere udfordringer end for ti år siden. De sensorer, de bruges med, har meget højere opløsningskrav, og formatstørrelser drives samtidig både mindre og større, mens pixelstørrelsen fortsætter med at skrumpe.
Tidligere begrænsede optikken aldrig billeddannelsessystemet, i dag gør det det. Hvor en typisk pixelstørrelse er omkring 9 µm, er en meget mere almindelig størrelse omkring 3 µm. Denne 81x stigning i priktæthed har taget sit præg på optikken, og selvom de fleste enheder er gode, er objektivvalg nu vigtigere end nogensinde.






