Jo ældre eleverne bliver, jo mere er der behov for hurtighed i at løse simple problemer. Der gives ikke meget tid i eksamener til at løse simple eksempler eller problemer i lang tid. Hvordan finder man diagonalen af en firkant hurtigt og nemt? Dette læres børn fra ottende klasse. Denne artikel viser to måder - den ene er længere, den anden er hurtigere.
Hvordan beregner man diagonalen af et kvadrat?
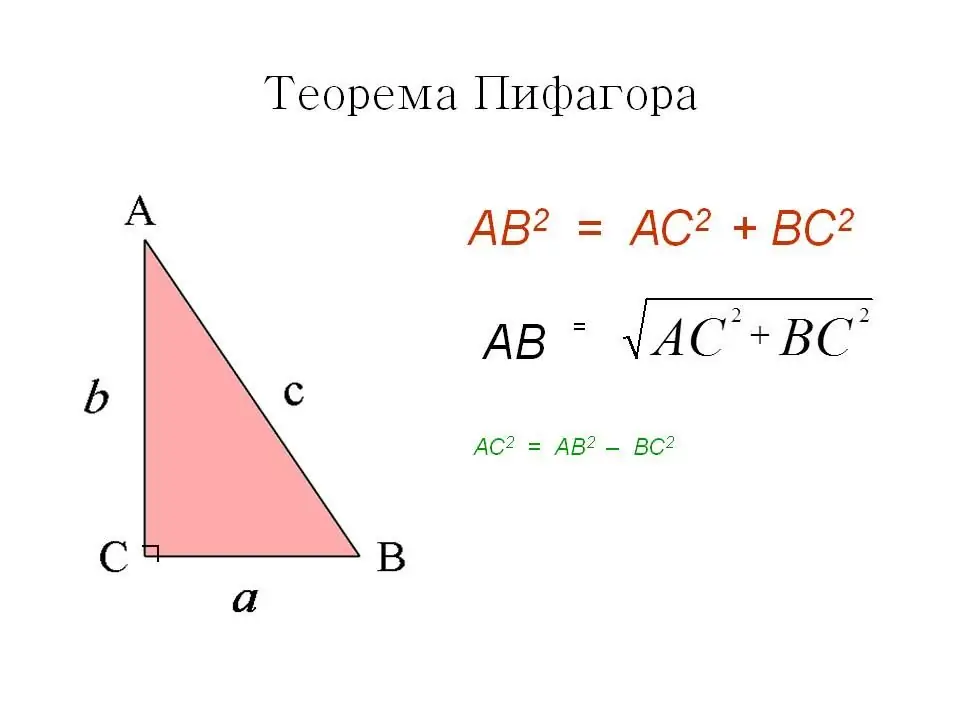
Den første måde er den velkendte og velkendte Pythagoras sætning. I et kvadrat er alle vinkler rette, hvilket betyder, at diagonalen deler den i to lige store retvinklede trekanter og selv er deres hypotenus. Ifølge Pythagoras sætning er hypotenusens kvadrat lig med summen af kvadraterne på benene.

Den anden måde er en simpel formel, der er unik for firkanter, og du skal bare huske den. Som du ved, er alle sider af et kvadrat ens, og derfor har matematikere beregnet følgende formel for at finde dens diagonal: den er lig med produktet af siden og roden af to.
Selvfølgelig er det bedst bare at huske formlen for længden af diagonalen af en firkant og altid bruge den, fordi det er meget hurtigere og mere bekvemt. Dette mærkes især, når man løser problemer i bogstavelig form, hvor man i stedet for hele store rodudtryk kun kan klare sig med ét produkt.
Eksempel
Tag for eksempel en kvadrat på 6 gange 6, det vil sige med en side svarende til seks centimeter.
Ifølge den første metode: lad diagonalen være C, og siden være A.
Så får vi, at C=√A^2+A^2 eller C=√2A^2.
Lad os skrive det i numerisk form: С=√36 + 36. Vi fik √72, hvilket er 3√8 eller 6√2.
Og lad os nu finde den samme diagonal, men ved den anden metode: C=A√2 eller i numerisk form: 6√2
Nu kan du se, hvor meget den anden metode er hurtigere, nemmere og vigtigst af alt - mere effektiv, især i så lette problemer, fordi hvert minut er dyrebart i eksamen!
Andre egenskaber ved firkantede diagonaler
Udover at vide, hvordan man finder diagonalerne af en firkant, skal du også kende deres egenskaber. De vigtigste er:
- Diagonalerne er lig med hinanden, og skæringspunktet er delt i to.
- De danner rette vinkler, når de skærer hinanden.
- Opdel firkanten i lige store trekanter.
Konklusion
Spørgsmålet om, hvordan man tæller diagonalerne af en firkant, bliver norm alt stillet af elever, der gik glip af dette emne i skolen. Men alle burde kende sådanne grundlæggende matematikregler! Det er ønskeligt at løse så hurtigt som muligt, og det kræver kendskab til forkortede formler. Alt dette er ekstremt enkelt og nemt, mensamtidig er det det nødvendige grundlag for at løse langt mere komplekse problemer i fremtiden. Og en vigtig del af denne base er pladsen.






