Isokorisk varmekapacitet for en ideel gas

2024 Forfatter: Angel Austin | [email protected]. Sidst ændret: 2023-12-17 05:21

I termodynamik er det vigtigt at kende processens termiske effekt, når man studerer overgange fra den indledende til den endelige tilstand af et system. Begrebet varmekapacitet er tæt forbundet med denne effekt. I denne artikel vil vi overveje spørgsmålet om, hvad der menes med en gass isokoriske varmekapacitet.

Ideel gas

En ideel gas er en gas, hvis partikler anses for at være materielle punkter, dvs. de har ikke dimensioner, men har masse, og hvori al indre energi udelukkende består af den kinetiske energi af molekylers bevægelse og atomer.

Enhver rigtig gas vil ideelt set aldrig tilfredsstille den beskrevne model, da dens partikler stadig har nogle lineære dimensioner og interagerer med hinanden ved hjælp af svage van der Waals-bindinger eller kemiske bindinger af en anden type. Men ved lave tryk og høje temperaturer er afstandene mellem molekyler store, og deres kinetiske energi overstiger den potentielle energi dusinvis af gange. Alt dette gør det muligt med en høj grad af nøjagtighed at anvende den ideelle model til rigtige gasser.

Intern energi af gas

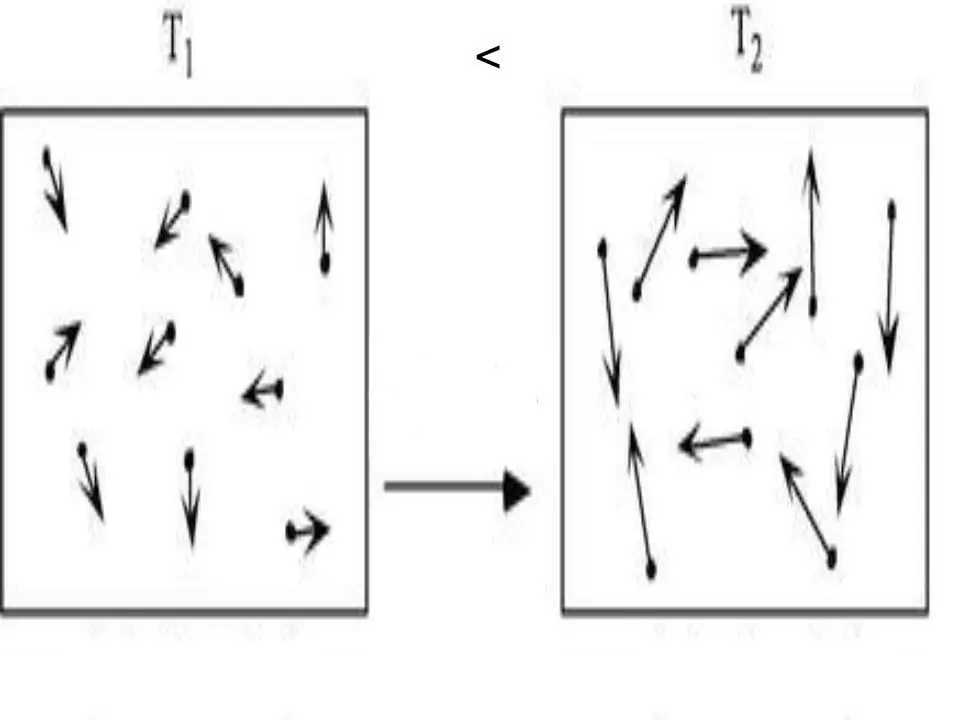
Den indre energi i ethvert system er en fysisk karakteristik, som er lig med summen af potentiel og kinetisk energi. Da potentiel energi kan forsømmes i ideelle gasser, kan vi skrive ligheden for dem:

U=E_k.

Hvor E_k er energien i det kinetiske system. Ved at bruge den molekylære kinetiske teori og anvende den universelle Clapeyron-Mendeleev tilstandsligning er det ikke svært at få et udtryk for U. Det er skrevet nedenfor:

U=z/2nRT.

Her er T, R og n henholdsvis den absolutte temperatur, gaskonstanten og mængden af stof. Z-værdien er et heltal, der angiver antallet af frihedsgrader, som et gasmolekyle har.

Isobarisk og isokorisk varmekapacitet

I fysik er varmekapacitet den mængde varme, der skal tilføres det undersøgte system for at opvarme det med en kelvin. Den omvendte definition er også sand, dvs. varmekapaciteten er den mængde varme, som systemet frigiver, når det afkøles med én kelvin.

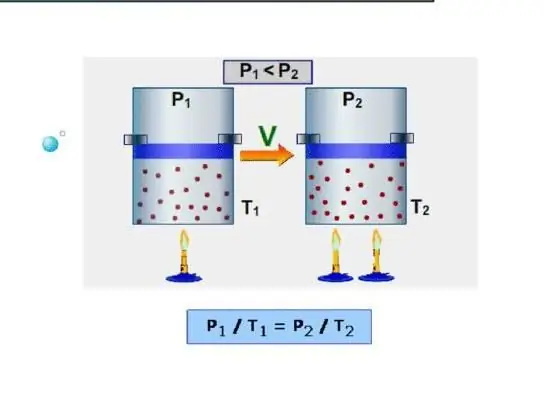
Den nemmeste måde for et system er at bestemme den isokoriske varmekapacitet. Det forstås som varmekapaciteten ved konstant volumen. Da systemet ikke udfører arbejde under sådanne forhold, bruges al energi på at øge interne energireserver. Lad os betegne den isokoriske varmekapacitet med symbolet C_V, så kan vi skrive:

dU=C_VdT.

Det vil sige ændringen i indre energisystemet er direkte proportional med ændringen i dets temperatur. Hvis vi sammenligner dette udtryk med ligheden skrevet i det foregående afsnit, så kommer vi frem til formlen for C_V i en ideel gasart:

С_V=z/2nR.

Denne værdi er ubelejlig at bruge i praksis, da den afhænger af mængden af stof i systemet. Derfor blev begrebet specifik isochorisk varmekapacitet introduceret, det vil sige en værdi, der beregnes enten pr. 1 mol gas eller pr. 1 kg. Lad os betegne den første værdi med symbolet C_V, den anden - med symbolet C_V m^{. For dem kan du skrive følgende formler:}

C_V=z/2R;

C_V^m=z/2R/M.

Her er M den molære masse.

Isobarisk er varmekapaciteten, mens der opretholdes et konstant tryk i systemet. Et eksempel på en sådan proces er udvidelsen af gas i en cylinder under et stempel, når den opvarmes. I modsætning til den isochoriske proces, bliver den varme, der tilføres systemet under den isobariske proces, brugt til at øge den indre energi og udføre mekanisk arbejde, det vil sige:

H=dU + PdV.

Entalpien af en isobarisk proces er produktet af den isobariske varmekapacitet og ændringen i temperaturen i systemet, det vil sige:

H=C_PdT.

Hvis vi betragter udvidelsen ved et konstant tryk på 1 mol gas, vil termodynamikkens første lov blive skrevet som:

C_PdT=C_V dT + RdT.

Det sidste led er hentet fra ligningenClapeyron-Mendeleev. Af denne lighed følger forholdet mellem isobariske og isokoriske varmekapaciteter:

C_P=C_V + R.

For en ideel gas er den specifikke molære varmekapacitet ved konstant tryk altid større end den tilsvarende isokoriske karakteristik med R=8, 314 J/(molK).

Frihedsgrader for molekyler og varmekapacitet

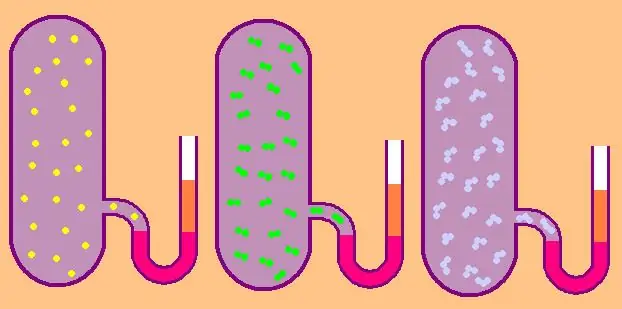
Lad os igen skrive formlen for den specifikke molære isochoriske varmekapacitet:

C_V=z/2R.

I tilfælde af en monoatomisk gas er værdien z=3, da atomer i rummet kun kan bevæge sig i tre uafhængige retninger.

Hvis vi taler om en gas bestående af diatomiske molekyler, for eksempel oxygen O₂ eller hydrogen H₂, så, ud over translationel bevægelse kan disse molekyler stadig rotere omkring to indbyrdes vinkelrette akser, dvs. z vil være lig med 5.

For mere komplekse molekyler, brug z=6. _{til at bestemme C}V