De naturlige fænomener og processer omkring os er ret komplekse. For deres nøjagtige fysiske beskrivelse bør der anvendes et besværligt matematisk apparat, og et stort antal væsentlige faktorer bør tages i betragtning. For at undgå dette problem bruges nogle forenklede modeller i fysik, som i høj grad letter den matematiske analyse af processen, men praktisk t alt ikke påvirker nøjagtigheden af dens beskrivelse. En af dem er den ideelle gasmodel. Lad os overveje det mere detaljeret i artiklen.
Konceptet med en ideel gas
En ideel gas er en tilstand af aggregering af et stof, som består af materielle punkter, der ikke interagerer med hinanden. Lad os forklare denne definition mere detaljeret.
For det første taler vi om materielle punkter som genstande, der udgør en ideel gas. Det betyder, at dets molekyler og atomer ikke har en størrelse, men har en vis masse. Den er feden tilnærmelse kan foretages under hensyntagen til det faktum, at i alle virkelige gasser ved lave tryk og høje temperaturer er afstanden mellem molekylerne meget større end deres lineære dimensioner.
For det andet bør molekylerne i en ideel gas ikke interagere med hinanden. I virkeligheden eksisterer sådanne interaktioner altid. Så selv atomer af ædelgasser oplever dipol-dipol-tiltrækning. Med andre ord er van der Waals interaktioner til stede. Sammenlignet med den kinetiske energi af rotation og translationel bevægelse af molekyler er disse interaktioner dog så små, at de ikke påvirker gassernes egenskaber. Derfor kan de ikke tages i betragtning ved løsning af praktiske problemer.
Det er vigtigt at bemærke, at ikke alle gasser, hvor densiteten er lav, og temperaturen er høj, kan betragtes som ideelle. Ud over van der Waals-interaktioner er der andre, stærkere typer bindinger, for eksempel hydrogenbindinger mellem H2O-molekyler, som fører til en grov krænkelse af gasidealitetsbetingelserne. Af denne grund er vanddamp ikke en ideel gas, men luft er det.
Fysisk model af en ideel gas
Denne model kan repræsenteres som følger: antag, at gassystemet indeholder N partikler. Disse kan være atomer og molekyler af forskellige kemikalier og grundstoffer. Antallet af N partikler er stort, så enheden "mol" bruges norm alt til at beskrive det (1 mol svarer til Avogadros tal). De bevæger sig alle i et eller andet volumen V. Partikelbevægelserer kaotiske og uafhængige af hinanden. Hver af dem har en vis hastighed v og bevæger sig langs en lige vej.
Teoretisk set er sandsynligheden for kollision mellem partikler næsten nul, da deres størrelse er lille sammenlignet med afstandene mellem partiklerne. Men hvis en sådan kollision opstår, så er den absolut elastisk. I sidstnævnte tilfælde bevares partiklernes samlede momentum og deres kinetiske energi.
Den betragtede model af ideelle gasser er et klassisk system med et stort antal elementer. Derfor adlyder hastigheden og energien af partikler i den den statistiske fordeling af Maxwell-Boltzmann. Nogle partikler har lave hastigheder, mens andre har høje hastigheder. I dette tilfælde er der en vis smal hastighedsgrænse, hvor de mest sandsynlige værdier af denne mængde ligger. Hastighedsfordelingen af nitrogenmolekyler er vist skematisk nedenfor.
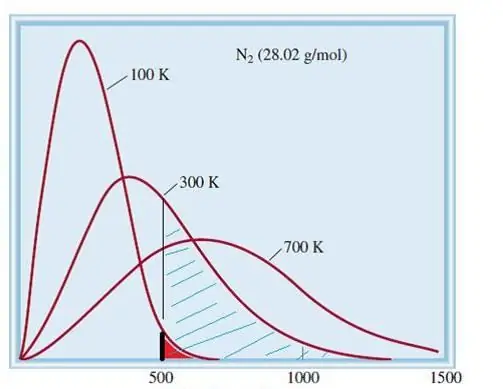
Kinetisk teori om gasser
Modellen af ideelle gasser beskrevet ovenfor bestemmer entydigt gassernes egenskaber. Denne model blev først foreslået af Daniel Bernoulli i 1738.

Derefter blev det udviklet til sin nuværende tilstand af August Kroenig, Rudolf Clausius, Mikhail Lomonosov, James Maxwell, Ludwig Boltzmann, Marian Smoluchowski og andre videnskabsmænd.
Den kinetiske teori om flydende stoffer, som den ideelle gasmodel er bygget på grundlag af, forklarer to vigtige makroskopiske egenskaber ved systemet baseret på dets mikroskopiske adfærd:
- Trykket i gasser er resultatet af partiklers kollision med karrets vægge.
- Temperaturen i systemet er resultatet af manifestationen af den konstante bevægelse af molekyler og atomer.
Lad os uddybe begge konklusioner af den kinetiske teori.
Gastryk
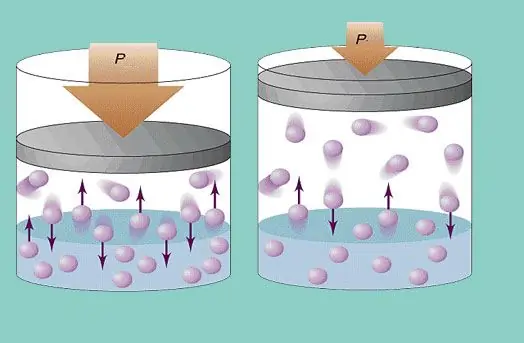
Den ideelle gasmodel forudsætter en konstant kaotisk bevægelse af partikler i systemet og deres konstante kollision med fartøjets vægge. Hver sådan kollision betragtes som absolut elastisk. Partikelmassen er lille (≈10-27-10-25 kg). Derfor kan den ikke skabe meget pres ved en kollision. Ikke desto mindre er antallet af partikler, og dermed antallet af kollisioner, enormt (≈1023). Derudover er grundstoffernes rodmiddelhastighed flere hundrede meter i sekundet ved stuetemperatur. Alt dette fører til skabelsen af et mærkbart tryk på fartøjets vægge. Det kan beregnes ved hjælp af følgende formel:
P=Nmvcp2 / (3V), hvor vcp er rodgennemsnitlig kvadrathastighed, m er partikelmasse.
Absolut temperatur
I henhold til den ideelle gasmodel er temperaturen entydigt bestemt af den gennemsnitlige kinetiske energi af et molekyle eller atom i det undersøgte system. Du kan skrive følgende udtryk, der relaterer kinetisk energi og absolut temperatur for en ideel gas:
mvcp2 / 2=3/2kB T.
Her er kB Boltzmann-konstanten. Fra denne lighed får vi:
T=m vcp2 / (3kB).
Universal tilstandsligning
Hvis vi kombinerer ovenstående udtryk for absolut tryk P og absolut temperatur T, kan vi skrive følgende lighed:
PV=nRT.
Her er n mængden af stof i mol, R er gaskonstanten introduceret af D. I. Mendeleev. Dette udtryk er den vigtigste ligning i teorien om ideelle gasser, fordi det kombinerer tre termodynamiske parametre (V, P, T) og ikke afhænger af gassystemets kemiske karakteristika.

Den universelle ligning blev først eksperimentelt udledt af den franske fysiker Emile Clapeyron i det 19. århundrede og derefter bragt til sin moderne form af den russiske kemiker Mendeleev, hvorfor den i øjeblikket bærer disse videnskabsmænds navne.






