I dag er der ikke et eneste sted tilbage på Jorden, som en person ikke har studeret eller i det mindste ikke har besøgt! Jo flere oplysninger der dukkede op om planetens overflade, jo mere presserende opstod spørgsmålet om at bestemme placeringen af et objekt. Meridianer og paralleller, som er elementer i gradgitteret, hjælper med at finde den geografiske adresse på det ønskede punkt og letter processen med at orientere sig på kortet.
Kartografiens historie
Menneskeheden kom ikke umiddelbart til en så simpel metode til at bestemme koordinaterne for et objekt som at beregne dets længde- og breddegrad. Velkendt for os alle fra skolen, dukkede hovedlinjerne gradvist op i kilderne til kartografisk viden. Nedenfor er information om flere vigtige stadier i historien om dannelsen af sådanne videnskaber som geografi og astronomi, som førte civilisationen til at skabe et moderne kort medpraktisk graticule.
En af naturvidenskabernes "forfædre" er Aristoteles, som var den første til at bevise, at vores planet har en sfærisk form

- Gamle rejsende på Jorden var meget opmærksomme, og de lagde mærke til, at på himlen (ved stjernerne), kan retningen C (nord) - syd (syd) let spores. Denne linje blev den første "meridian", hvis analog i dag kan findes på det enkleste kort.
- Eratosthenes, der er bedre kendt som "geografividenskabens fader", gjorde en masse små og store opdagelser, der påvirkede dannelsen af geodæsi. Han var den første til at bruge et skafis (gammelt solur) til at beregne solens højde over forskellige byers territorium og bemærkede en betydelig forskel i hans målinger, som afhang af tidspunktet på dagen og årstiden. Eratosthenes afslørede sammenhængen mellem videnskaber som geodæsi og astronomi og gjorde det derved muligt at udføre mange undersøgelser og målinger af terrestriske territorier ved hjælp af himmellegemer.

Graticule
Talrige meridianer og paralleller, der skærer hinanden på et kort eller en globus, er forbundet til et geografisk gitter bestående af "firkanter". Hver af dens celler er begrænset af linjer, der har deres egen grad. Ved hjælp af dette gitter kan du således hurtigt finde det ønskede objekt. Strukturen af mange atlass er bygget på en sådan måde, at forskellige firkanter betragtes på separate sider, hvilket gør det muligt systematisk at studere ethvert territorium. Med udviklinggeografisk viden forbedret og kloden. Meridianer og paralleller er tilgængelige på de allerførste modeller, som, selvom de ikke indeholdt alle pålidelige oplysninger om jordens objekter, allerede gav en idé om den omtrentlige placering af de ønskede punkter. Moderne kort har obligatoriske elementer, der udgør gradgitteret. Det bruges til at bestemme koordinaterne.
Graticule-elementer
- poler - nord (ovenfor) og syd (under) er de punkter, hvor meridianerne konvergerer. De er udgangspunkterne for den virtuelle linje, som kaldes aksen.
- Polarcirkler. Grænserne for polarområderne begynder med dem. De polarcirkler (syd og nord) er placeret yderligere 23 paralleller mod polerne.
- Nul meridian. Den deler Jordens overflade i den østlige og vestlige halvkugle og har yderligere to navne: Greenwich og Initial. Alle meridianer har samme længde og forbinder polerne på overfladen af en globus eller et kort.
- Ækvator. Det er den længste parallel, orienteret fra W (vest) til E (øst), som deler planeten i den sydlige og nordlige halvkugle. Alle andre linjer parallelt med ækvator har forskellige størrelser - deres længde aftager mod polerne.
- Troperne. Der er også to af dem - Stenbukken (Syd) og Kræften (nord). Troperne er placeret ved den 66. breddegrad syd og nord for ækvator.
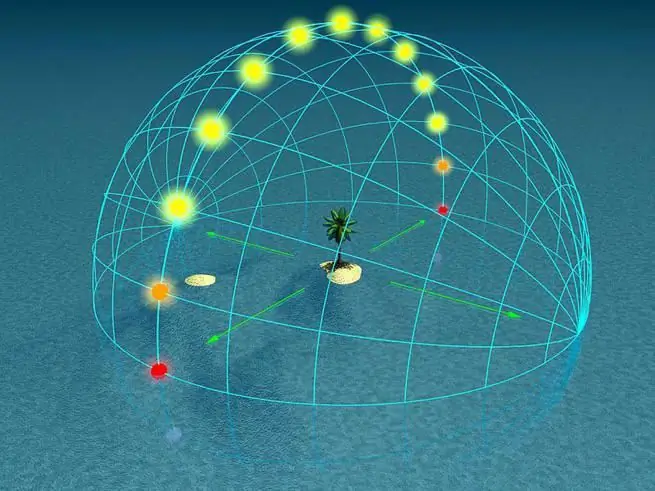
Hvordan bestemmes meridianerne og parallellerne for det ønskede punkt?
Hvert objekt på vores planet har sin egen bredde- og længdegrad! Også selvom han er megetmeget lille eller omvendt ret stor! At bestemme et objekts meridianer og paralleller og finde et punkts koordinater er en og samme handling, da det er graden af hovedlinjerne, der bestemmer den geografiske adresse på det ønskede territorium. Nedenfor er en handlingsplan, som du kan bruge, når du beregner koordinaterne.
Algorithme til at bestemme den geografiske adresse for et objekt på kortet
- Tjek det korrekte geografiske navn på objektet. Irriterende fejl opstår på grund af banal uopmærksomhed, for eksempel: en elev lavede en fejl i navnet på det ønskede punkt og bestemte de forkerte koordinater.
- Få en satin, skarp blyant eller markør og forstørrelsesglas klar. Disse værktøjer hjælper dig med mere præcist at bestemme adressen på det objekt, du leder efter.
- Vælg det største kort fra atlasset, der indeholder det ønskede geografiske punkt. Jo mindre skala kortet er, jo flere fejl opstår i beregningerne.
- Bestem forholdet mellem objektet og hovedelementerne i gitteret. Algoritmen for denne procedure præsenteres efter afsnittet: "Beregning af størrelsen af territoriet".
- Hvis det ønskede punkt ikke er placeret direkte på linjen angivet på kortet, så find de nærmeste, der har en digital betegnelse. Gradlinjer er norm alt angivet langs omkredsen af kortet, sjældnere - på ækvatorlinjen.
- Når du bestemmer koordinaterne, er det vigtigt at finde ud af, hvor mange grader parallellerne og meridianerne er placeret på kortet og beregne de nødvendige korrekte. Det skal huskes, at elementerne i gratiklen, bortset fra hovedlinjerne, kan trækkes gennem ethvert punkt på overfladenJorden.
Beregn størrelsen af området
- Hvis du skal beregne størrelsen af et objekt i kilometer, så skal du huske, at længden af en grad af gitterlinjer er - 111 km.
- For at bestemme længden af et objekt fra W til E (hvis det er helt placeret i en af halvkuglerne: østlig eller vestlig), er det nok at trække den mindre værdi fra den større værdi af bredden af en af yderpunkterne og gange det resulterende tal med 111 km.
- Hvis du skal beregne længden af territoriet fra N til S (kun hvis det hele er placeret i en af halvkuglerne: sydlige eller nordlige), så skal du trække den mindre fra den større grad af længdegraden af et af yderpunkterne, multiplicer derefter det modtagede beløb for 111 km.
- Hvis Greenwich-meridianen passerer gennem objektets territorium, så for at beregne dens længde fra W til E, tilføjes breddegraderne for de ekstreme punkter i denne retning, så multipliceres deres sum med 111 km.
- Hvis ækvator er placeret på territoriet for det objekt, der defineres, så for at bestemme længden fra N til S, er det nødvendigt at tilføje længdegraderne for de ekstreme punkter i denne retning og gange den resulterende beløb med 111 km.
Hvordan bestemmer man forholdet mellem et objekt og hovedelementerne i graticulaen?
- Hvis objektet er under ækvator, vil dets bredde kun være syd, hvis det er over - nord.
- Hvis det ønskede punkt er placeret til højre for den indledende meridian, vil dets længde være øst, hvis det er til venstre - vest.
- Hvis et objekt er placeret over den 66. grads nordlige eller sydlige breddegrad, er det inkluderet itilsvarende polarområde.
Beregning af koordinaterne for bjerge
Da mange bjergsystemer har en stor udstrækning i forskellige retninger, og meridianerne og parallellerne, der krydser sådanne objekter, har forskellige grader, er processen med at bestemme deres geografiske adresse ledsaget af mange spørgsmål. Nedenfor er muligheder for at beregne koordinaterne for de høje territorier i Eurasien.

Kaukasus
De mest maleriske bjerge ligger mellem to vandområder på fastlandet: fra Sortehavet til Det Kaspiske Hav. Kaukasusbjergenes meridianer og paralleller har forskellige grader, så hvilke skal betragtes som afgørende for adressen på dette system? I dette tilfælde fokuserer vi på det højeste punkt. Det vil sige, at koordinaterne for Kaukasus-bjergsystemet er den geografiske adresse på Elbrus-toppen, som er lig med 42 grader 30 minutter nordlig bredde og 45 grader østlig længde.

Himalaya
Det højeste system af bjerge på vores fastland er Himalaya. Meridianer og paralleller, der har forskellige grader, krydser dette objekt lige så ofte som ovenstående. Hvordan bestemmer man korrekt koordinaterne for dette system? Vi handler på samme måde som i tilfældet med Uralbjergene, vi fokuserer på systemets højeste punkt. Koordinaterne for Himalaya falder således sammen med adressen på Chomolungma-toppen, og dette er 29 grader 49 minutter nordlig bredde og 83 grader 23 minutter og 31 sekunder østlig længde.

Uralbjergene
Uralbjergene er de længste på vores fastland. Meridianer og paralleller, der har forskellige grader, skærer dette objekt i forskellige retninger. For at bestemme koordinaterne for Uralbjergene skal du finde deres centrum på kortet. Dette punkt vil være den geografiske adresse på dette objekt - 60 grader nordlig bredde og samme østlige længde. Denne metode til at bestemme koordinaterne for bjerge er acceptabel for systemer, der har en stor udstrækning i en af retningerne eller i begge retninger.






