Hvert skolebarn ved, at lys i et homogent gennemsigtigt medie bevæger sig ad en lige vej. Denne kendsgerning giver os mulighed for at overveje mange optiske fænomener inden for rammerne af begrebet lysstråle. Denne artikel taler om strålens indfaldsvinkel, og hvorfor det er vigtigt at kende denne vinkel.
En lysstråle er en mikrometer elektromagnetisk bølge
I fysik er der bølger af forskellig art: lyd, hav, elektromagnetisk og nogle andre. Udtrykket "stråle" gælder dog kun for elektromagnetiske bølger, som det synlige spektrum er en del af. Selve ordet "stråle" kan repræsenteres som en lige linje, der forbinder to punkter i rummet.
Lys (som en bølge) kan ses som en lige linje, fordi hver bølge indebærer tilstedeværelsen af vibrationer. Svaret på dette spørgsmål ligger i værdien af bølgelængden. Så for marine og lyd varierer længden fra et par centimeter til snesevis af meter. Naturligvis kan sådanne svingninger næppe kaldes en stråle. Lysets bølgelængde er mindre end en mikrometer. Det menneskelige øje er ikke i stand til at skelne sådanne vibrationer, derfor forekommer det os detat vi ser en direkte stråle.
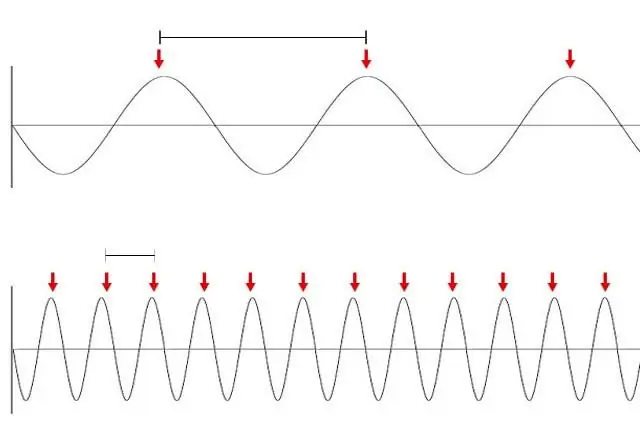
For fuldstændighedens skyld skal det bemærkes, at lysstrålen kun er synlig, når den begynder at sprede sig på små partikler, såsom i et støvet rum eller tågedråber.
Hvor er det vigtigt at kende vinklen, hvormed strålen rammer forhindringen?
Fænomenerne refleksion og brydning er de mest berømte optiske effekter, som en person støder på bogstaveligt t alt hver dag, når han ser sig selv i spejlet eller drikker et glas te efter at have set på skeen i det.
Den matematiske beskrivelse af brydning og refleksion kræver viden om strålens indfaldsvinkel. For eksempel er fænomenet refleksion karakteriseret ved ligheden mellem reflektionsvinklen og indfaldsvinklen. Hvis beskrevet fra siden af brydningsprocessen, er indfaldsvinklen og brydningsvinklen relateret til hinanden gennem funktionerne af sinus og mediernes brydningsindeks (Snells lov)..

Vinklen, hvormed en lysstråle falder på grænsefladen mellem to transparente medier, spiller en vigtig rolle, når man overvejer effekten af intern total refleksion i et optisk tættere materiale. Denne effekt observeres kun i tilfælde af indfaldsvinkler, der er større end en kritisk værdi.
Geometrisk definition af den betragtede vinkel
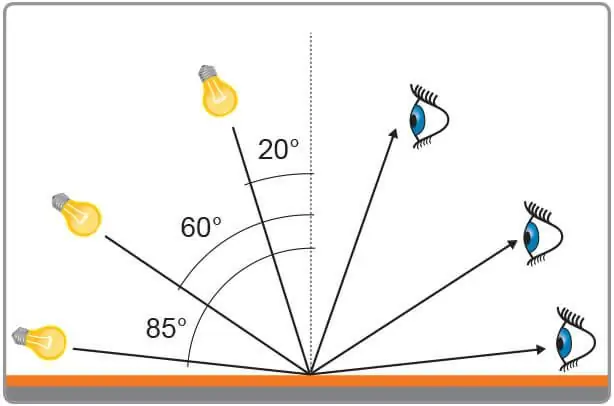
Det kan antages, at der er en eller anden overflade, der adskiller de to miljøer. Denne overflade kan være flad, som i tilfældet med et spejl, eller den kan være mere kompleks, såsom havets rillede overflade. Forestil dig, at på denne overflade falderlysstråle. Hvordan bestemmer man lysindfaldsvinklen? At gøre dette er ret simpelt. Det følgende er en række handlinger, der skal udføres for at finde den ønskede vinkel.
- Først skal du bestemme skæringspunktet mellem strålen og overfladen.
- Gennem O skal man tegne en vinkelret på den betragtede overflade. Det kaldes ofte norm alt.
- Strålens indfaldsvinkel er lig med vinklen mellem den og normalen. Det kan måles med en simpel vinkelmåler.
Som du kan se, er det ikke svært at finde den overvejede vinkel. Eleverne begår dog ofte den fejl at måle det mellem flyet og strålen. Det skal huskes, at indfaldsvinklen altid måles ud fra normalen, uanset overfladens form og det medium, den forplanter sig i.
Sfæriske spejle, linser og stråler, der falder på dem
Kendskab til egenskaberne ved visse strålers indfaldsvinkler bruges til konstruktion af billeder i sfæriske spejle og tynde linser. For at bygge sådanne billeder er det nok at vide, hvordan to forskellige stråler opfører sig, når de interagerer med de navngivne optiske enheder. Skæringspunktet mellem disse stråler bestemmer billedpunktets position. I det generelle tilfælde kan man altid finde tre forskellige stråler, hvis forløb er nøjagtigt kendt (den tredje stråle kan bruges til at kontrollere rigtigheden af det konstruerede billede). Disse stråler er navngivet nedenfor.
- Kører parallelt med enhedens optiske hovedakse. Den passerer gennem fokus efter refleksion eller brydning.
- En stråle, der passerer gennem enhedens fokus. Det afspejler altidbrydes parallelt med hovedaksen.
- Gennem det optiske center (for et sfærisk spejl falder det sammen med midten af kuglen, for en linse er det inde i det). Sådan en stråle ændrer ikke sin bane.
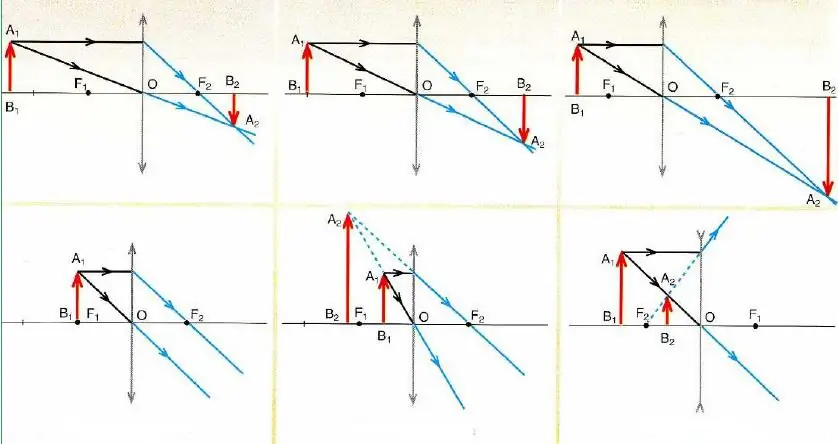
Figuren ovenfor viser skemaerne til at konstruere billeder for forskellige muligheder for objektets placering i forhold til tynde linser.






