Gasser, fra termodynamikkens synspunkt, er beskrevet af et sæt makroskopiske karakteristika, hvoraf de vigtigste er temperatur, tryk og volumen. Konstansen af en af disse parametre og ændringen i de to andre indikerer, at en eller anden isoproces forekommer i gassen. Vi vil afsætte denne artikel til et detaljeret svar på spørgsmålene om, at dette er en isokorisk proces, hvordan den adskiller sig fra isotermiske og isobariske ændringer i et gassystems tilstand.
Ideel gas i fysik

Før du besvarer spørgsmålet om, at dette er en isokorisk proces, bør du lære begrebet en ideel gas bedre at kende. I fysik forstås det som enhver gas, hvor den gennemsnitlige kinetiske energi af dens bestanddele langt overstiger den potentielle energi af deres interaktion, og afstandene mellem disse partikler er flere størrelsesordener større end deres lineære dimensioner. Under de nævnte forhold er det muligt, når du udførerberegninger tager ikke hensyn til vekselvirkningsenergien mellem partikler (den er lig med nul), og det kan også antages, at partiklerne er materialepunkter med en vis masse m.
Den eneste proces, der finder sted i en ideel gas, er kollisionen af partikler med væggene i beholderen, der indeholder stoffet. Disse kollisioner viser sig i praksis som eksistensen af et vist tryk i gassen P.
Som regel kan ethvert gasformigt stof, der består af relativt kemisk inerte molekyler, og som har lavt tryk og høje temperaturer, betragtes som en ideel gas med tilstrækkelig nøjagtighed til praktiske beregninger.
Ligning, der beskriver en ideel gas
Vi taler selvfølgelig om Clapeyron-Mendeleevs universelle lov, som bør forstås godt for at forstå, at dette er en isochorisk proces. Så den universelle tilstandsligning har følgende form:
PV=nRT.
Det vil sige, at produktet af trykket P og gasvolumenet V er lig med produktet af den absolutte temperatur T og mængden af stof i mol n, hvor R er proportionalitetsfaktoren. Selve ligningen blev første gang skrevet ned af Emile Clapeyron i 1834, og i 70'erne af det 19. århundrede erstattede D. Mendeleev et sæt konstante værdier af en enkelt universel gaskonstant R (8.314 J/(molK))).
I overensstemmelse med Clapeyron-Mendeleev-ligningen forbliver antallet af gaspartikler konstant i et lukket system, så der er kun tre makroskopiske parametre, der kan ændre sig (T, Pog V). Det sidste faktum ligger til grund for forståelsen af de forskellige isoprocesser, som vil blive diskuteret nedenfor.
Hvad er en isokorisk proces?
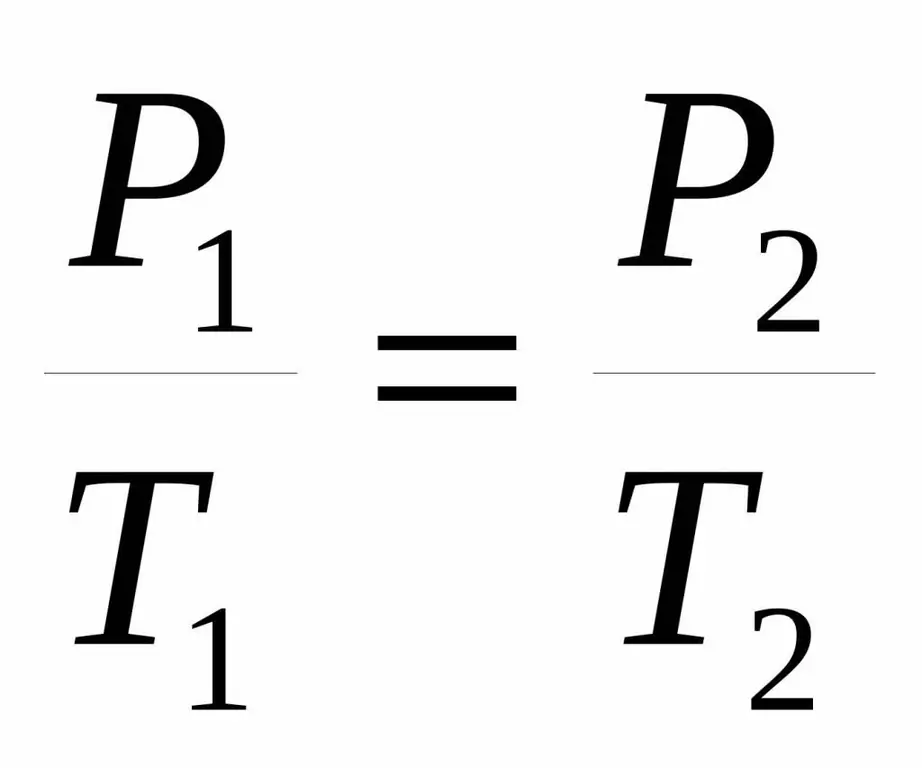
Denne proces forstås som absolut enhver ændring i systemets tilstand, hvor dets volumen bevares.
Hvis vi vender os til den universelle tilstandsligning, kan vi sige, at i en isokorisk proces kun tryk og absolut temperatur ændrer sig i en gas. For at forstå præcis, hvordan de termodynamiske parametre ændrer sig, skriver vi det tilsvarende matematiske udtryk:
P / T=konstant.
Nogle gange gives denne lighed i en lidt anden form:
P1 / T1=P2 / T 2.
Begge ligheder kaldes Charles' lov efter navnet på en fransk videnskabsmand, der i slutningen af det 18. århundrede opnåede den bemærkede afhængighed eksperimentelt.

Hvis vi bygger en graf af funktionen P(T), så får vi en retlinet afhængighed, som kaldes en isochore. Enhver isochore (for alle værdier af n og V) er en lige linje.
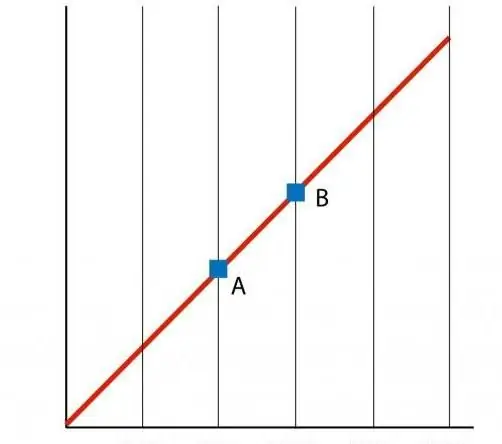
Energibeskrivelse af processen
Som nævnt er en isochorisk proces en ændring i et systems tilstand, der finder sted i et lukket, men ikke isoleret system. Vi taler om muligheden for varmeudveksling mellem gassen og miljøet. Generelt fører enhver tilførsel af varme Q til systemet til to resultater:
- ændrer intern energi U;
- gasvirker A, udvider eller trækker sammen.
Den sidste slutning skrives matematisk som følger:
Q=U + A.
Den isokoriske proces af en ideel gas, ifølge sin definition, indebærer ikke arbejde udført af gassen, da dens volumen forbliver uændret. Det betyder, at al den varme, der leveres til systemet, går til at øge dets interne energi:
Q=U.
Hvis vi erstatter den eksplicitte formel for intern energi i dette udtryk, så kan varmen fra den isochoriske proces repræsenteres som:
Q=z / 2nRT.
Her er z antallet af frihedsgrader, som er bestemt af den polyatomiske natur af de molekyler, der udgør gassen. For en monoatomisk gas er z=3, for en diatomisk gas - 5, og for en triatomisk gas - 6. Her mener vi under frihedsgrader translationelle og rotationsgrader.
Hvis vi sammenligner effektiviteten af opvarmning af et gassystem i isochoriske og isobariske processer, så vil vi i det første tilfælde få den maksimale effektivitet, da gassen udvider sig under den isobariske ændring i systemets tilstand, og en del af varmetilførslen bruges på at udføre arbejde.
Isobarisk proces
Ovenfor har vi beskrevet i detaljer, at dette er en isochorisk proces. Lad os nu sige et par ord om andre isoprocesser. Lad os starte med isobarisk. Ud fra navnet forstås det som overgangen af systemet mellem tilstande ved konstant tryk. Denne proces er beskrevet af Gay-Lussac-loven som følger:
V / T=konst.
Som med isochore repræsenterer V(T)-isobaren også en ret linje på grafen.
Foraf enhver isobarisk proces, er det bekvemt at beregne arbejdet udført af gassen, da det er lig med produktet af konstant tryk og ændringen i volumen.
Isotermisk proces
Dette er en proces, hvor systemets temperatur forbliver konstant. Det er beskrevet af Boyle-Mariotte-loven for en ideel gas. Det er underligt at bemærke, at dette er den første eksperimentelt opdagede gaslov (anden halvdel af det 17. århundrede). Dens matematiske notation ser sådan ud:
PV=konst.
Isokoriske og isotermiske processer adskiller sig med hensyn til deres grafiske repræsentation, da funktionen P(V) er en hyperbolsk, ikke en lineær sammenhæng.
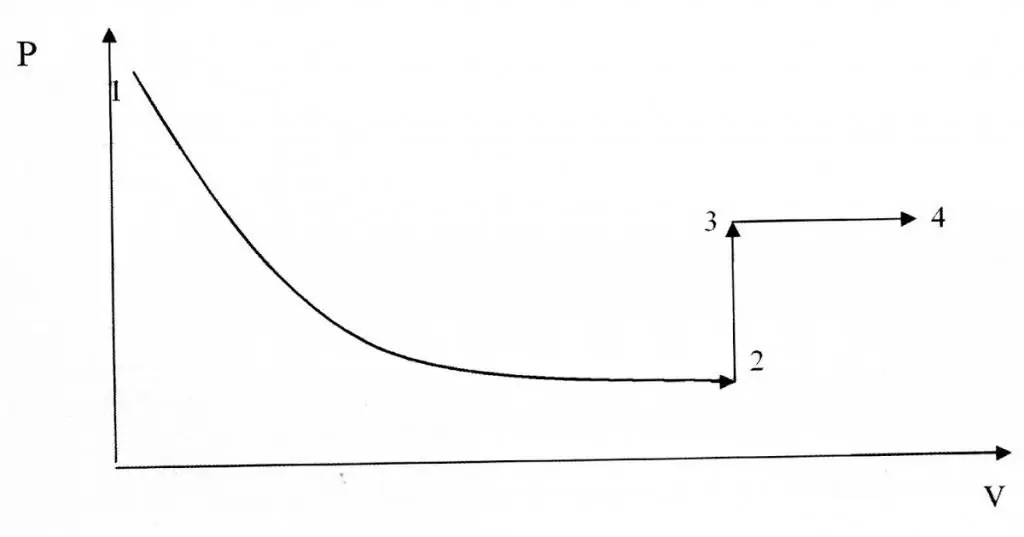
Eksempel på problemløsning
Lad os konsolidere de teoretiske oplysninger i artiklen ved deres anvendelse for at løse et praktisk problem. Det er kendt, at rent gasformigt nitrogen var i en cylinder ved et tryk på 1 atmosfære og en temperatur på 25 °C. Efter at gasflasken var opvarmet og trykket i den blev målt, viste det sig at være 1,5 atmosfærer. Hvad er temperaturen på gassen i cylinderen efter opvarmning? Hvor meget ændrede gassens indre energi sig, hvis der var 4 mol nitrogen i ballonen.
For at besvare det første spørgsmål bruger vi følgende udtryk:
P1 / T1=P2 / T 2.
Hvorfra vi kommer:
T2=P2 / P1 T 1.
I dette udtryk kan tryk erstattes i vilkårlige enhedermålinger, da de krymper, og temperaturen kun er i kelvin. Når det er sagt, får vi:
T2=1,5 /1298,15=447,224 K.
Den beregnede temperatur i grader Celsius er 174 °C.
Da nitrogenmolekylet er diatomisk, kan ændringen i dets indre energi under opvarmning bestemmes som følger:
ΔU=5 / 2nRΔT.
Ved at erstatte de kendte værdier i dette udtryk, får vi svaret på det andet spørgsmål i problemet: ΔU=+12,4 kJ.






