Jeg synes, vi skal starte med historien om et så herligt matematisk værktøj som differentialligninger. Som alle differential- og integralregninger blev disse ligninger opfundet af Newton i slutningen af det 17. århundrede. Han anså netop denne opdagelse af ham for så vigtig, at han endda krypterede beskeden, som i dag kan oversættes sådan her: "Alle naturlove er beskrevet af differentialligninger." Dette kan virke som en overdrivelse, men det er sandt. Enhver lov om fysik, kemi, biologi kan beskrives med disse ligninger.

Matematikerne Euler og Lagrange ydede et stort bidrag til udviklingen og skabelsen af teorien om differentialligninger. Allerede i det 18. århundrede opdagede og udviklede de det, de nu studerer på universiteternes seniorkurser.
En ny milepæl i studiet af differentialligninger begyndte takket være Henri Poincare. Han skabte en "kvalitativ teori om differentialligninger", som i kombination med teorien om funktioner for en kompleks variabel ydede et væsentligt bidrag til grundlaget for topologi - videnskaben om rummet og detsejendomme.

Hvad er differentialligninger?
Mange mennesker er bange for én sætning "differentialligning". Men i denne artikel vil vi detaljere hele essensen af dette meget nyttige matematiske apparat, som faktisk ikke er så kompliceret, som det ser ud til ud fra navnet. For at begynde at tale om førsteordens differentialligninger, bør du først sætte dig ind i de grundlæggende begreber, der i sagens natur er relateret til denne definition. Og vi starter med differentialet.
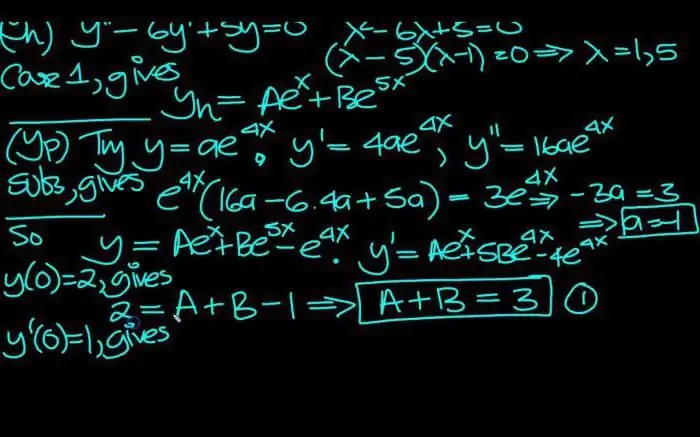
Differential
Mange kender dette koncept fra skolen. Lad os dog se nærmere på det. Forestil dig en graf over en funktion. Vi kan øge det i en sådan grad, at et hvilket som helst af dets segmenter vil tage form af en lige linje. På den tager vi to punkter, der er uendeligt tæt på hinanden. Forskellen mellem deres koordinater (x eller y) vil være en uendelig lille værdi. Det kaldes en differential og er betegnet med tegnene dy (differential fra y) og dx (differential fra x). Det er meget vigtigt at forstå, at differentialet ikke er en endelig værdi, og dette er dens betydning og hovedfunktion.
Og nu skal vi overveje det næste element, som vil være nyttigt for os til at forklare konceptet med en differentialligning. Dette er den afledte.
Afledt
Vi har sikkert alle hørt i skolen og dette koncept. Den afledte siges at være væksthastigheden eller faldet af en funktion. Dog ud fra denne definitionmeget bliver uklart. Lad os prøve at forklare den afledte i form af differentialer. Lad os gå tilbage til et infinitesim alt segment af en funktion med to punkter, der er i minimum afstand fra hinanden. Men selv for denne afstand formår funktionen at ændre sig en del. Og for at beskrive denne ændring fandt de frem til en afledet, som ellers kan skrives som et forhold mellem differentialer: f(x)'=df/dx.
Nu er det værd at overveje derivatets grundlæggende egenskaber. Der er kun tre af dem:
- Den afledte af summen eller forskellen kan repræsenteres som summen eller forskellen af afledte: (a+b)'=a'+b' og (a-b)'=a'-b'.
- Den anden egenskab er relateret til multiplikation. Den afledte af et produkt er summen af produkterne af en funktion og den afledede af en anden: (ab)'=a'b+ab'.
- Den afledte forskel kan skrives som følgende lighed: (a/b)'=(a'b-ab')/b2.
Alle disse egenskaber vil være nyttige til at finde løsninger på førsteordens differentialligninger.
Der er også partielle derivater. Lad os sige, at vi har en funktion z, der afhænger af variablene x og y. For at beregne den partielle afledede af denne funktion, f.eks. med hensyn til x, skal vi tage variablen y som en konstant og simpelthen differentiere.
Integral
Et andet vigtigt koncept er integralen. Faktisk er dette det direkte modsatte af derivatet. Der er flere typer integraler, men for at løse de simpleste differentialligninger har vi brug for de mest trivielle ubestemte integraler.
Så hvad er et integral? Lad os sige, at vi har en vis afhængighed ffra x. Vi tager integralet fra det og får funktionen F (x) (ofte kaldet antiderivatet), hvis afledte er lig med den oprindelige funktion. Således F(x)'=f(x). Det følger også heraf, at integralet af den afledede er lig med den oprindelige funktion.
Når man løser differentialligninger, er det meget vigtigt at forstå betydningen og funktionen af integralet, da man bliver nødt til at tage dem meget ofte for at finde løsningen.
Ligninger er forskellige afhængigt af deres natur. I det næste afsnit vil vi overveje typerne af førsteordens differentialligninger og derefter lære at løse dem.
Klasser af differentialligninger
"Diffury" er opdelt efter rækkefølgen af de derivater, der er involveret i dem. Således er der den første, anden, tredje og mere rækkefølge. De kan også opdeles i flere klasser: ordinære og partielle afledte.
I denne artikel vil vi overveje almindelige differentialligninger af første orden. Vi vil også diskutere eksempler og måder at løse dem på i de følgende afsnit. Vi vil kun overveje ODE'er, fordi disse er de mest almindelige ligningstyper. Almindelige er opdelt i underarter: med adskillelige variabler, homogene og heterogene. Dernæst vil du lære, hvordan de adskiller sig fra hinanden, og lære, hvordan du løser dem.
Desuden kan disse ligninger kombineres, så vi efter får et system af differentialligninger af første orden. Vi vil også overveje sådanne systemer og lære, hvordan man løser dem.
Hvorfor overvejer vi kun den første ordre? For du skal starte med en simpel en og beskrive alt relateret til differentialligninger, i én artikel er simpelthen umuligt.

Separable variabelligninger
Dette er måske de enkleste førsteordens differentialligninger. Disse omfatter eksempler, der kan skrives således: y'=f(x)f(y). For at løse denne ligning har vi brug for en formel til at repræsentere den afledede som et forhold mellem differentialer: y'=dy/dx. Ved at bruge det får vi følgende ligning: dy/dx=f(x)f(y). Nu kan vi vende os til metoden til at løse standardeksempler: vi deler variablerne op i dele, dvs. vi overfører alt med y-variablen til den del, hvor dy er placeret, og vi vil gøre det samme med x-variablen. Vi får en ligning af formen: dy/f(y)=f(x)dx, som løses ved at tage integralerne af begge dele. Glem ikke konstanten, der skal indstilles efter at have taget integralet.
Løsningen til enhver "diffurance" er en funktion af afhængigheden af x af y (i vores tilfælde), eller, hvis der er en numerisk betingelse, så er svaret i form af et tal. Lad os analysere hele løsningsforløbet ved hjælp af et specifikt eksempel:
y'=2ysin(x)
Flyt variabler i forskellige retninger:
dy/y=2sin(x)dx
Nu tager vi integraler. Alle kan findes i en speciel tabel over integraler. Og vi får:
ln(y)=-2cos(x) + C
Hvis det kræves, kan vi udtrykke "y" som en funktion af "x". Nu kan vi sige, at vores differentialligning er løst, hvis der ikke er givet nogen betingelse. En betingelse kan gives, f.eks. y(n/2)=e. Så erstatter vi simpelthen værdien af disse variable i løsningen ogfind værdien af konstanten. I vores eksempel er det lig med 1.
Førsteordens homogene differentialligninger
Nu til den sværere del. Homogene differentialligninger af første orden kan skrives i generel form som følger: y'=z(x, y). Det skal bemærkes, at den rigtige funktion af to variable er homogen, og den kan ikke opdeles i to afhængigheder: z på x og z på y. At kontrollere, om ligningen er homogen eller ej, er ret simpel: Vi laver substitutionen x=kx og y=ky. Nu aflyser vi alle k. Hvis alle disse bogstaver reduceres, så er ligningen homogen, og du kan trygt fortsætte med at løse den. Lad os sige fremad: princippet om at løse disse eksempler er også meget enkelt.
Vi skal lave en substitution: y=t(x)x, hvor t er en funktion, der også afhænger af x. Så kan vi udtrykke den afledede: y'=t'(x)x+t. Ved at indsætte alt dette i vores oprindelige ligning og forenkle den, får vi et eksempel med adskillelige variable t og x. Vi løser det og får afhængigheden t(x). Da vi fik det, erstatter vi blot y=t(x)x i vores tidligere erstatning. Så får vi afhængigheden af y af x.
For at gøre det klarere, lad os se på et eksempel: xy'=y-xey/x.
Når du tjekker med udskiftning, er alt reduceret. Så ligningen er virkelig homogen. Nu laver vi en anden substitution, som vi t alte om: y=t(x)x og y'=t'(x)x+t(x). Efter forenkling får vi følgende ligning: t'(x)x=-et. Vi løser det resulterende eksempel med adskilte variable og får: e-t=ln(Cx). Vi behøver kun at erstatte t med y/x (trods alt, hvis y=tx, så t=y/x), og vi fårsvar: e-y/x=ln(xC).

Førsteordens lineære differentialligninger
Det er tid til endnu et stort emne. Vi vil analysere inhomogene differentialligninger af første orden. Hvordan adskiller de sig fra de to foregående? Lad os finde ud af det. Lineære differentialligninger af første orden i generel form kan skrives som følger: y' + g(x)y=z(x). Det er værd at præcisere, at z(x) og g(x) kan være konstanter.
Og nu et eksempel: y' - yx=x2.
Der er to måder at løse det på, og vi vil håndtere begge i rækkefølge. Den første er metoden til variation af vilkårlige konstanter.
For at løse ligningen på denne måde, skal du først sidestille højre side med nul og løse den resulterende ligning, som efter at have flyttet delene vil have formen:
y'=yx;
dy/dx=yx;
dy/y=xdx;
ln|y|=x2/2 + C;
y=ex2/2yC=C1ex2/2.
Nu skal vi erstatte konstanten C1 med funktionen v(x), som vi skal finde.
y=vex2/2.
Lad os ændre den afledede:
y'=v'ex2/2-xvex2/2.
Og indsæt disse udtryk i den oprindelige ligning:
v'ex2/2 - xvex2/2 + xvex2 /2 =x2.
Du kan se, at to termer annullerer i venstre side. Hvis det i et eksempel ikke skete, så har du gjort noget forkert. Fortsæt:
v'ex2/2 =x2.
Nu løser vi den sædvanlige ligning, hvor vi skal adskille variablerne:
dv/dx=x2/ex2/2;
dv=x2e-x2/2dx.
For at udtrække integralet er vi nødt til at anvende integration af dele her. Dette er dog ikke emnet for vores artikel. Hvis du er interesseret, kan du lære, hvordan du selv udfører sådanne handlinger. Det er ikke svært, og med tilstrækkelig dygtighed og opmærksomhed tager det ikke meget tid.
Lad os vende os til den anden metode til at løse inhomogene ligninger: Bernoulli-metoden. Hvilken tilgang der er hurtigere og nemmere er op til dig.
Så, når vi løser ligningen med denne metode, skal vi lave en erstatning: y=kn. Her er k og n nogle x-afhængige funktioner. Så vil den afledede se således ud: y'=k'n+kn'. Indsæt begge substitutioner i ligningen:
k'n+kn'+xkn=x2.
Gruppe:
k'n+k(n'+xn)=x2.
Nu skal vi sætte lig med nul, hvad der står i parentes. Hvis du nu kombinerer de to resulterende ligninger, får du et system af førsteordens differentialligninger, som du skal løse:
n'+xn=0;
k'n=x2.
Den første lighed løses som en normal ligning. For at gøre dette skal du adskille variablerne:
dn/dx=xv;
dn/n=xdx.
Tag integralet og få: ln(n)=x2/2. Så hvis vi udtrykker n:
n=ex2/2.
Nu erstatter vi den resulterende lighed i systemets anden ligning:
k'ex2/2=x2.
Og ved at transformere får vi den samme lighed som i den første metode:
dk=x2/ex2/2.
Vi vil heller ikke gå ind i yderligere trin. Det er værd at sige, at løsningen af førsteordens differentialligninger først forårsager betydelige vanskeligheder. Men efterhånden som du dykker dybere ned i emnet, begynder det at blive bedre og bedre.
Hvor bruges differentialligninger?
Differentialligninger bruges meget aktivt i fysik, da næsten alle grundlæggende love er skrevet i differentialform, og de formler, vi ser, er løsningen af disse ligninger. I kemi bruges de af samme grund: grundlæggende love er afledt af dem. I biologi bruges differentialligninger til at modellere opførsel af systemer, såsom rovdyr-bytte. De kan også bruges til at skabe reproduktionsmodeller af f.eks. en koloni af mikroorganismer.
Hvordan vil differentialligninger hjælpe i livet?
Svaret på dette spørgsmål er enkelt: ingen måde. Hvis du ikke er videnskabsmand eller ingeniør, er det usandsynligt, at de er nyttige for dig. Men for generel udvikling skader det ikke at vide, hvad en differentialligning er, og hvordan den løses. Og så spørgsmålet om en søn eller datter "hvad er en differentialligning?" vil ikke forvirre dig. Nå, hvis du er en videnskabsmand eller en ingeniør, så forstår du selv vigtigheden af dette emne i enhver videnskab. Men det vigtigste er, at nu spørgsmålet "hvordan løser man en førsteordens differentialligning?" du kan altid svare. Enig, det er altid rartnår du forstår, hvad folk overhovedet er bange for at forstå.
Vigtigste læringsproblemer
Hovedproblemet med at forstå dette emne er den ringe evne til at integrere og differentiere funktioner. Hvis du er dårlig til at tage afledte og integraler, så skal du nok lære mere, mestre forskellige metoder til integration og differentiering og først derefter begynde at studere det materiale, der blev beskrevet i artiklen.
Nogle mennesker bliver overraskede, når de finder ud af, at dx kan overføres, for tidligere (i skolen) blev det oplyst, at brøken dy/dx er udelelig. Her skal du læse litteraturen om den afledede og forstå, at det er forholdet mellem uendelige små størrelser, der kan manipuleres, når man løser ligninger.
Mange indser ikke umiddelbart, at løsningen af førsteordens differentialligninger ofte er en funktion eller et integral, der ikke kan tages, og denne vrangforestilling giver dem mange problemer.
Hvad ellers kan studeres for en bedre forståelse?
Det er bedst at begynde yderligere fordybelse i differentialregningens verden med specialiserede lærebøger, for eksempel i calculus for studerende med ikke-matematiske specialer. Så kan du gå videre til mere specialiseret litteratur.
Det skal siges, at der udover differentialligninger også er integralligninger, så du vil altid have noget at stræbe efter og noget at studere.

Konklusion
Vi håber, at efter at have læstDenne artikel gav dig en idé om, hvad differentialligninger er, og hvordan du løser dem korrekt.
Under alle omstændigheder vil matematik på en eller anden måde være nyttig for os i livet. Det udvikler logik og opmærksomhed, uden hvilken enhver person er som uden hænder.






