Naturlige geometriske mønstre eller mønstre fremstår som gentagne former, der nogle gange kan beskrives eller repræsenteres af matematiske modeller.
Geometri i naturen og livet findes i mange former og former, såsom symmetri, spiraler eller bølger.
Historie
For første gang tog oldgræske filosoffer og videnskabsmænd - Pythagoras, Empedocles og Platon - spørgsmål om geometri i naturen op. Ved at analysere eksempler på forudsigelige eller ideelle geometriske former i planter og dyr forsøgte de at demonstrere orden og symmetri i naturen.
Moderne forsøg på at studere geometri i naturen begyndte i det 19. århundrede med indsatsen fra den belgiske fysiker Joseph Plateau, som udviklede konceptet om minimumsoverfladen af en sæbeboble. De første moderne forsøg koncentrerede sig først om at demonstrere ideelle og forudsigelige geometriske former og vendte sig derefter mod udviklingen af modeller, der forudsiger udseendet og manifestationen af geometri i naturen.
I det 20. århundrede arbejdede matematiker Alan Turing med mekanismerne for morfogenese, som forklarer udseendet hos dyrforskellige mønstre, striber, pletter. Lidt senere vil biologen Aristide Lindenmeier sammen med matematikeren Benoit Mandelbrot færdiggøre arbejdet med matematiske fraktaler, der gentog vækstmønstrene for nogle planter, herunder træer.
Science
Moderne videnskaber (matematik, fysik og kemi) forsøger ved hjælp af teknologier og modeller ikke kun at forklare, men også at forudsige de geometriske mønstre, der findes i naturen.
Formen og farven på mange levende organismer, såsom påfugle, kolibrier og havskaller, er ikke kun smukke, men også geometrisk korrekte, hvilket tiltrækker videnskabsmænds nysgerrighed. Den skønhed, vi observerer i naturen, kan være forårsaget naturligt, matematisk.
De observerede naturlige mønstre i matematik forklares af kaosteori, som arbejder med spiraler og fraktaler. Sådanne mønstre adlyder fysikkens love, derudover forudsiger fysik og kemi, ved hjælp af abstrakt matematik, formen af krystaller, både naturlige og kunstige.
Biologi forklarer geometrien i naturen ved naturlig udvælgelse, hvor sådanne regelmæssige karakteristika som striber, pletter, lyse farver kan forklares med behovet for maskering eller afsendelse af signaler.
Typer af mønstre
I naturen er der mange gentagne mønstre, der optræder i forskellige geometriske former. Typer af basale regelmæssigheder af geometri i naturen, fotos og deres beskrivelser kan findes nedenfor.
Symmetri. Denne geometriske form er en af de mest almindelige i naturen. Mest almindelig hos dyrspejlsymmetri - sommerfugle, biller, tigre, ugler. Det findes også i planter, såsom ahornblade eller orkidéblomster. Derudover kan symmetrisk geometri i naturen være radial, femstrålet eller seksdobbelt, ligesom snefnug.

Fraktaler. I matematik er disse selv-lignende konstruktioner, der er uendelige. I naturen er det umuligt at opdage en sådan endeløs selvgentagende form, derfor kaldes tilnærmelser af fraktale mønstre geometriske fraktaler i naturen. Sådan geometri kan observeres i naturen i bregneblade, broccoli, ananasfrugter.
Spiraler. Disse former er især almindelige blandt bløddyr og snegle. Forskere observerer spiralformer i rummet, for eksempel spiralgalakser. Spiralen kaldes Fibonaccis gyldne snit.

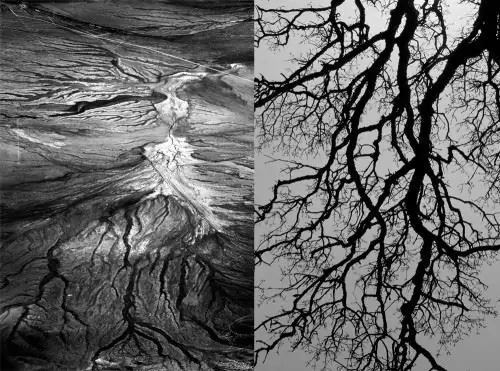
Meanders. Tilfældigheden af dynamiske systemer i matematik manifesterer sig i naturen i sådanne former som bugter og strømninger. Naturlig geometri har form af en brudt eller snarere buet linje, såsom en flodstrøm.
Bølger. De er forårsaget af forstyrrelser og bevægelser af luft, vindstrømme, spredt både gennem luft og gennem vand. I naturen er det ikke kun havbølger, men også ørkenklitter, som kan danne geometriske former - linjer, halvmåner og parabler.
mosaik. Skabt ved at gentage de samme elementer på overfladen. Mosaikgeometri i dyrelivet findes i bier: de byggerbikube af honningkager - gentagne celler.

Formation af mønstre
I biologi skyldes dannelsen af en geometrisk farve processen med naturlig udvælgelse. Tilbage i midten af det 20. århundrede lykkedes det Alan Turing at beskrive mekanismen for fremkomsten af pletter og striber i dyrenes farve – han kaldte det reaktions-diffusionsmodellen. Visse celler i kroppen indeholder gener, der styres af kemiske reaktioner. Morfogen fører til dannelsen af hudområder med mørkt pigment (pletter og striber). Hvis morfogenet er til stede i alle hudceller - fås panterens farve, hvis det er ujævnt - den sædvanlige plettede leopard.






