Hvad er forbindelsen mellem musik og eksakte videnskaber, som matematik? Folk har stillet dette spørgsmål siden oldtiden. Moderne videnskabsmænd har bevist, at de mentale processer, der opstår ved løsning af matematiske problemer, ligner dem, der opstår under fremførelsen af musikværker og studiet af emner i den musikteoretiske cyklus.
For eksempel er at bestemme musikalske intervaller ved gehør, at finde afstanden mellem lyde med forskellige tonehøjder. Baseret på dette blev det konkluderet, at det parallelle studie af musik og matematik i høj grad kan lette assimileringen af begge videnskaber.

Der er også en åbenlys lighed mellem nogle elementer af musikteoretisk og matematisk terminologi. Dette skyldes til dels brugen i begge videnskaber af en række udtryk af latinsk oprindelse, men ikke desto mindre finder en sådan lighed sted. Denne artikel giver definitionerintervaller fra et musikteoretisk synspunkt og svaret på spørgsmålet: hvad er intervaller i matematik. Også i artiklen er der eksempler på brugen af udtrykket "interval" i nogle andre områder.
Generelt koncept
Tænk først på selve betydningen af ordet "interval" og dets oprindelse.
Så hvad er intervaller?
Ordet "interval" har latinske rødder og kan oversættes som et mellemrum eller en afstand. Dette udtryk, ud over musik og matematik, bruges i sådanne vidensområder som: militære anliggender (angiver afstanden mellem to militærpersoner, militære enheder såvel som mellem enheder af militært udstyr), medicin (bruges i kardiografi), er af central betydning i relativitetsteorien, bruges i timing af oversvømmelser, vulkanudbrud og lignende naturfænomener.
Hvad er intervaller i musik?
I musikteoretiske discipliner er et interval i ordets brede betydning afstanden mellem to musikalske lyde og i snæver forstand konsonansen af to lyde, der kan afspilles samtidigt eller sekventielt. Hvis lydene af et interval tages samtidigt, betragtes et sådant interval som harmonisk, og hvis det er sekventielt, er det melodisk.

Musikintervaller kan udtrykkes både i matematiske tal, der angiver antallet af trin i intervallet, og i akustiske enheder - cents. Intervaller har latinske navne, alt efter antallet af skalatrin, der er indeholdt i dem: prima(oversat som "første") - et trin, et andet ("andet") - to trin, og så videre. De kan også være enkle og sammensatte. Der er otte simple intervaller (en oktav og alle intervaller mindre end den).
I betragtning af spørgsmålet om, hvad intervaller er i musik, er det værd at nævne en værdi mere, der kendetegner dem, nemlig antallet af halvtoner indeholdt i dem. På dette grundlag er intervallerne opdelt i store og små, rene, reducerede og øgede.
Andre funktioner i musikalske intervaller
Inversion af et interval er overførslen af dets lavere lyd en oktav op. Samtidig ændres den kvalitative komponent til det modsatte - store bliver til små, øges til mindre og så videre. Rene intervaller bliver altid kun til rene. Summen af de numeriske betegnelser for konsonanser konverteret til hinanden er ni.

Således bliver prima en oktav, den tredje bliver til en sjette og så videre. For sammensatte intervaller er reglerne noget anderledes: intervallets to lyde skal flyttes en oktav, den øverste en oktav op, og bunden af intervallet en oktav ned. Summen af de digitale betegnelser i dette tilfælde skal være lig med tallet seksten.
Forholdet mellem de to videnskaber
Fra de tidligere oplysninger er det klart, at musikteoretisk viden i høj grad er baseret på matematiske beregninger. Så fordelen ved parallel undersøgelse af begge discipliner er indlysende. Når alt kommer til alt, løser elever fra musikalske uddannelsesinstitutioner problemer i harmoniklasser, jeg bruger det sammearitmetiske beregninger. Med undtagelse af de glade ejere af den såkaldte "absolute pitch", for hvem dette arbejde i høj grad er lettet af naturlige evner.

Fordelene ved musiktimer for udvikling af matematiske evner og udvikling af logisk tænkning generelt blev eksperimentelt bekræftet af den ungarske innovative lærer Zoltan Kodaly i midten af forrige århundrede.
Han grundlagde flere skoler med dybdegående studier af musik. Desuden blev antallet af musiktimer øget ved at reducere timerne til andre fag. Et kontroltværsnit udført i alle fag i slutningen af uddannelsescyklussen afslørede et vidensniveau hos elever på forsøgsskoler, der oversteg kendskabet hos elever i traditionelle skoler.
Hvad er intervaller i matematik?
I matematisk videnskab bruges to udtryk oftest, betegnet med ordet "interval". Definitionerne af disse to begreber udgør svaret på spørgsmålet: hvad er intervaller set fra den matematiske videnskabs synspunkt.

Så det mest almindelige i matematik er intervallerne for monotoni og konstanthed. Overvej deres definitioner.
Hvad er monotoniske intervaller?
Dette er intervaller for værdien af funktionsargumentet, hvor funktionen kun bliver stigende eller kun faldende.
Hvad er konstansintervaller?
Dette er intervaller af definitionsdomænet, hvor fortegnet for funktionen forbliver uændret.
I beggetilfælde taler vi om bestemte intervaller, som i tilfælde af musikalske intervaller.
Det måske mest slående eksempel på brugen af ordet "interval" i en specifik branche er det velkendte computerprogram "Word". Lad os studere dette øjeblik. Hvad er intervaller i Word?
Brug i "Word"
Det er kendt, at tre typer huller er involveret i dette program:
- Mellemrum mellem linjer.
- Mellem separate afsnit.
- Mellem tilstødende sider.
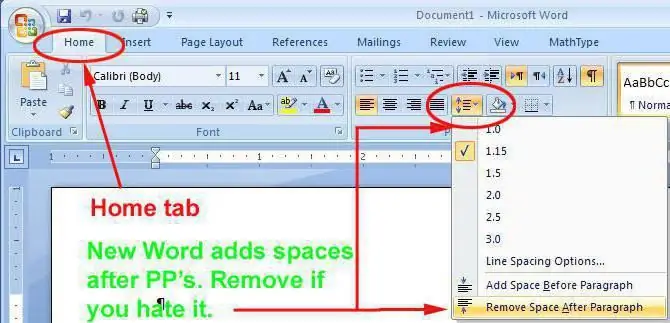
Der er ingen grund til at overveje i detaljer betydningen af hvert af de ovennævnte tre intervaller, der bruges i Word-programmet, da meget litteratur er viet til dette. Det er kun værd at bemærke, at vi i dette tilfælde taler om et fænomen, der har, omend fjernt, men lighed med musikalske intervaller.
Afslutningsvis
Denne artikel diskuterede forholdet mellem musik og matematik. Det blev afsløret, at en sådan sammenhæng virkelig eksisterer, hvilket bevises både ved eksperimenter i pædagogisk videnskab og ved analyse af tankeprocesser i begge typer aktiviteter. Spørgsmålet om, hvad intervaller er i musik og matematik, overvejes også. Også her afsløres nogle fællespunkter i definitionerne af matematiske og musikalske termer. Nu står det klart, hvad intervaller er. Og dette beviser endnu en gang, at kontaktområdet mellem de to sfærer, matematik og musik, virkelig eksisterer.






