Som du ved, hører enhver fysisk størrelse til en af to typer, den er enten skalær eller vektor. I denne artikel vil vi overveje sådanne kinematiske karakteristika som hastighed og acceleration og også vise, hvor accelerations- og hastighedsvektorerne er rettet.
Hvad er hastighed og acceleration?
Begge mængderne nævnt i dette afsnit er vigtige kendetegn ved enhver form for bevægelse, uanset om det drejer sig om at bevæge en krop i en lige linje eller langs en buet bane.
Speed er den hastighed, hvormed koordinaterne ændres over tid. Matematisk er denne værdi lig med den tidsafledte af den tilbagelagte distance, dvs.:
v¯=dl¯/dt.
Her er vektoren l¯ rettet fra startpunktet for stien til slutpunktet.
Til gengæld er acceleration den hastighed, hvormed selve hastigheden ændres over tid. I form af en formel kan det skrives sådan:
a¯=dv¯/dt.
Det er klart, at tage den anden afledede afforskydningsvektor l¯ med tiden, vil vi også få værdien af accelerationen.
Da hastigheden måles i meter pr. sekund, måles acceleration, ifølge det skrevne udtryk, i meter pr. sekund i anden kvadrat.

Hvor er accelerations- og hastighedsvektorerne?
I fysik er enhver mekanisk bevægelse af en krop norm alt karakteriseret ved en bestemt bane. Sidstnævnte er en imaginær kurve, langs hvilken kroppen bevæger sig i rummet. For eksempel er en lige linje eller en cirkel gode eksempler på almindelige bevægelsesbaner.
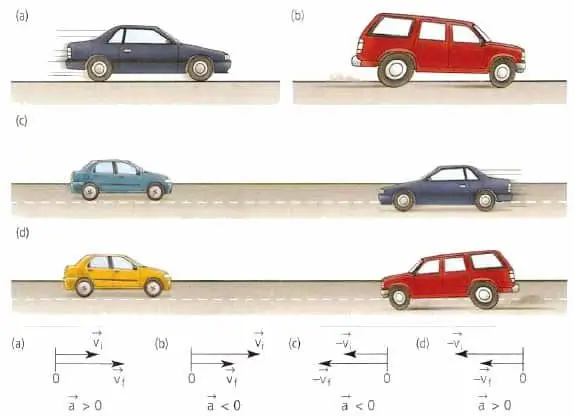
Kroppens hastighedsvektor er altid rettet i bevægelsesretningen, uanset om kroppen sænker farten eller accelererer, om den bevæger sig i en lige linje eller langs en kurve. Når man taler i geometriske termer, er hastighedsvektoren rettet tangentielt til punktet af den bane, hvori kroppen aktuelt befinder sig.
Accelerationsvektoren for et materiale eller kropspunkt har intet at gøre med hastighed. Denne vektor er rettet i retning af hastighedsændring. For retlinet bevægelse kan værdien a¯ f.eks. enten falde sammen i retning med v¯ eller være modsat v¯.
Tving, der virker på kroppen og acceleration
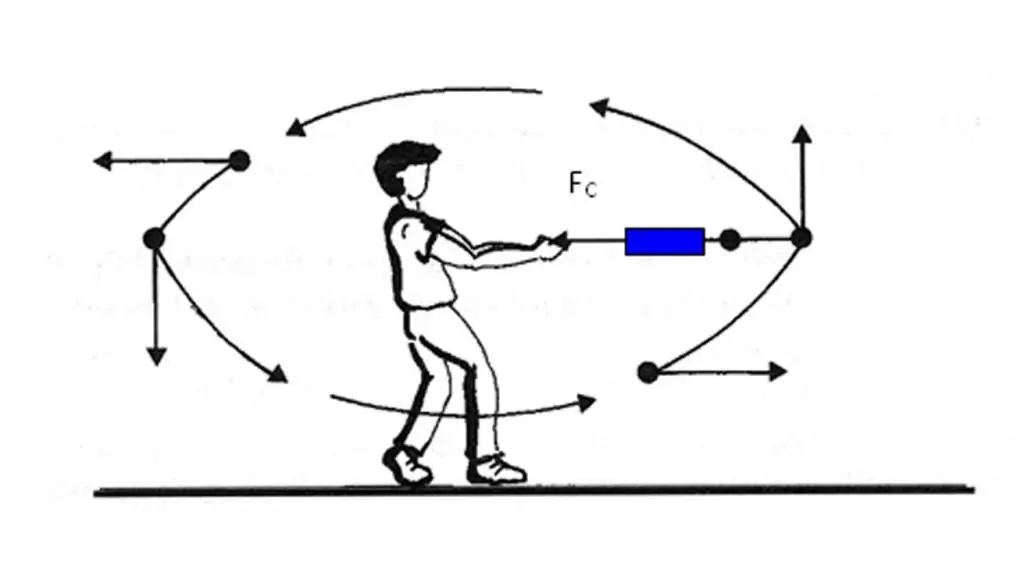
Vi har fundet ud af, at kroppens accelerationsvektor er rettet mod ændringen af hastighedsvektoren. Det er dog ikke altid nemt at afgøre, hvordan hastigheden ændrer sig på et givet punkt i banen. Desuden er det nødvendigt at udføre operationen for at bestemme ændringen i hastighedenvektor forskelle. For at undgå disse vanskeligheder med at bestemme retningen af vektoren a¯, er der en anden måde at finde ud af det hurtigt.
Nedenfor er Newtons berømte og velkendte lov til enhver studerende:
F¯=ma¯.
Formlen viser, at årsagen til acceleration i legemer er kraften, der virker på dem. Da massen m er en skalar, er kraftvektoren F¯ og accelerationsvektoren a¯ i samme retning. Dette faktum bør huskes og anvendes i praksis, når der er behov for at bestemme retningen for mængden a¯.
Hvis flere forskellige kræfter virker på kroppen, så vil retningen af accelerationsvektoren være lig med den resulterende vektor af alle kræfter.
Cirkulær bevægelse og acceleration
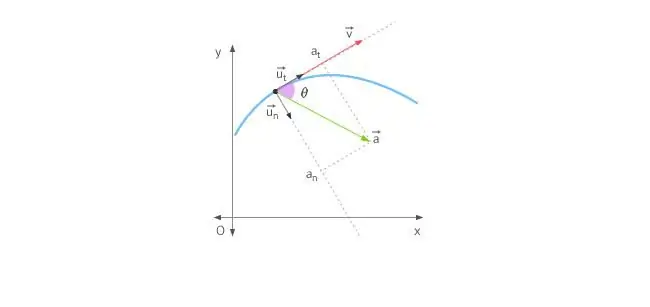
Når en krop bevæger sig i en lige linje, er accelerationen rettet enten fremad eller bagud. I tilfælde af bevægelse i en cirkel kompliceres situationen af, at hastighedsvektoren konstant ændrer retning. I lyset af ovenstående er den totale acceleration bestemt af dens to komponenter: tangentielle og normale accelerationer.
Tangentialacceleration er rettet nøjagtigt det samme som hastighedsvektoren eller mod den. Med andre ord er denne accelerationskomponent rettet langs tangenten til banen. Tangentiel acceleration beskriver ændringen i modulet af selve hastigheden.
Normal acceleration er rettet langs normalen til det givne punkt på banen, under hensyntagen til dens krumning. I tilfælde af cirkulær bevægelse indikerer vektoren af denne komponenttil centrum, det vil sige, at den normale acceleration er rettet langs rotationsradius. Denne komponent kaldes ofte centripetal.
Fuld acceleration er summen af disse komponenter, så dens vektor kan rettes vilkårligt i forhold til cirkellinjen.
Hvis kroppen roterer uden at ændre den lineære hastighed, er der kun en normalkomponent, der ikke er nul, så den fulde accelerationsvektor er rettet mod cirklens centrum. Bemærk, at dette center også er påvirket af en kraft, der holder kroppen på sin bane. Solens gravitationskraft holder f.eks. vores Jord og andre planeter i deres kredsløb.






