Når man studerede egenskaberne for en andengradsligning, blev der sat en restriktion - for en diskriminant mindre end nul er der ingen løsning. Det blev straks fastsat, at vi taler om et sæt reelle tal. En matematikers nysgerrige sind vil være interesseret - hvad er hemmeligheden i klausulen om virkelige værdier?
Med tiden introducerede matematikere begrebet komplekse tal, hvor den betingede værdi af den anden rod af minus en tages som en enhed.
Historisk baggrund
Matematisk teori udvikler sig sekventielt, fra simpel til kompleks. Lad os finde ud af, hvordan konceptet kaldet "komplekst tal" opstod, og hvorfor det er nødvendigt.
Fra umindelige tider var grundlaget for matematik den sædvanlige beretning. Forskerne kendte kun det naturlige værdisæt. Addition og subtraktion var enkle. Efterhånden som økonomiske relationer blev mere komplekse, begyndte man at bruge multiplikation i stedet for at tilføje de samme værdier. Der er en omvendt operation tilmultiplikation - division.
Begrebet et naturligt tal begrænsede brugen af aritmetiske operationer. Det er umuligt at løse alle divisionsproblemer på sættet af heltalsværdier. Arbejdet med brøker førte først til begrebet rationelle værdier og derefter til irrationelle værdier. Hvis det for det rationelle er muligt at angive den nøjagtige placering af punktet på linjen, så er det for det irrationelle umuligt at angive et sådant punkt. Du kan kun anslå intervallet. Foreningen af rationelle og irrationelle tal dannede et reelt sæt, som kan repræsenteres som en bestemt linje med en given skala. Hvert trin langs linjen er et naturligt tal, og mellem dem er rationelle og irrationelle værdier.
Teoretisk matematiks æra er begyndt. Udviklingen af astronomi, mekanik, fysik krævede løsningen af mere og mere komplekse ligninger. Generelt blev rødderne til andengradsligningen fundet. Ved løsning af et mere komplekst kubisk polynomium stødte forskerne ind i en selvmodsigelse. Konceptet med en terningrod fra en negativ giver mening, men for en kvadratrod opnås usikkerhed. Desuden er andengradsligningen kun et speci altilfælde af den kubiske ligning.
I 1545 foreslog italieneren J. Cardano at introducere begrebet et imaginært tal.

Dette tal er den anden rod af minus én. Udtrykket komplekst tal blev endelig dannet kun tre hundrede år senere, i værker af den berømte matematiker Gauss. Han foreslog formelt at udvide alle algebralovene til det imaginære tal. Den rigtige linje er blevet udvidet tilfly. Verden er større.
Grundlæggende begreber
Hent en række funktioner, der har begrænsninger på det rigtige sæt:
- y=arcsin(x), defineret mellem negativ og positiv 1.
- y=ln(x), decimallogaritme giver mening med positive argumenter.
- kvadratrod y=√x, kun beregnet for x ≧ 0.
Betegner i=√(-1), vi introducerer et sådant koncept som et imaginært tal, dette vil fjerne alle restriktioner fra definitionsdomænet for ovenstående funktioner. Udtryk som y=arcsin(2), y=ln(-4), y=√(-5) giver mening i et eller andet rum med komplekse tal.
Den algebraiske form kan skrives som et udtryk z=x + i×y på mængden af reelle x- og y-værdier, og i2 =-1.
Det nye koncept fjerner alle restriktioner for brugen af enhver algebraisk funktion og ligner en graf af en ret linje i koordinater af reelle og imaginære værdier.
Kompleks fly
Den geometriske form af komplekse tal giver os visuelt mulighed for at repræsentere mange af deres egenskaber. På Re(z)-aksen markerer vi de reelle x-værdier, på Im(z) - de imaginære værdier af y, så vil z-punktet på planet vise den nødvendige komplekse værdi.
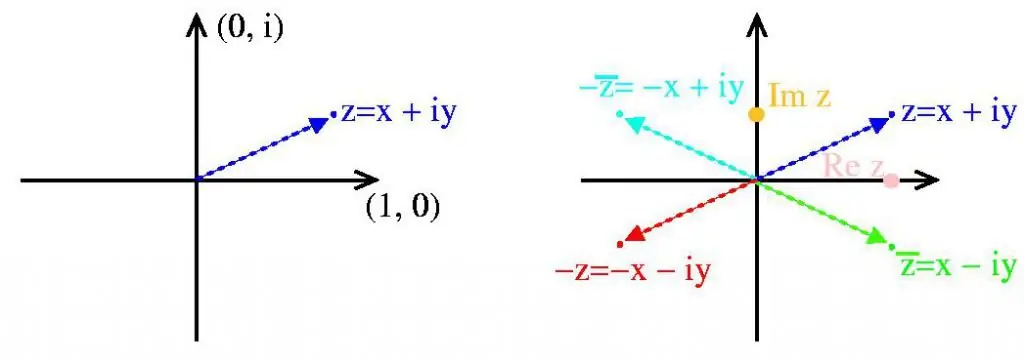
Definitioner:
- Re(z) - reel akse.
- Im(z) - betyder den imaginære akse.
- z - betinget punkt i et komplekst tal.
- Den numeriske værdi af længden af vektoren fra nul til z kaldesmodul.
- Ægte og imaginære akser opdeler flyet i kvarte. Med en positiv værdi af koordinaterne - I kvartal. Når argumentet for den reelle akse er mindre end 0, og den imaginære akse er større end 0 - II kvart. Når koordinaterne er negative - III kvartal. Det sidste, fjerde kvartal indeholder mange positive reelle værdier og negative imaginære værdier.
På et plan med x- og y-koordinatværdier kan man således altid visualisere et punkt med et komplekst tal. Tegnet i introduceres for at adskille den virkelige del fra den imaginære.
Properties
- Når værdien af det imaginære argument er nul, får vi kun et tal (z=x), som er placeret på den reelle akse og hører til den reelle mængde.
- Særtilfælde, når værdien af det reelle argument bliver nul, svarer udtrykket z=i×y til placeringen af punktet på den imaginære akse.
- Den generelle form for z=x + i×y vil være for værdier der ikke er nul for argumenterne. Angiver placeringen af punktet, der karakteriserer det komplekse tal i et af kvartalerne.
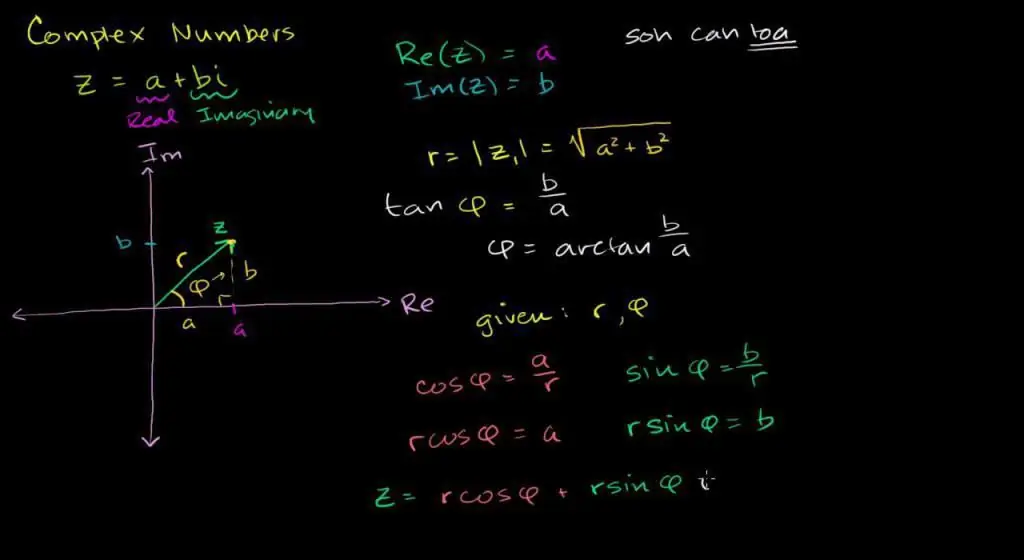
Trigonometrisk notation
Hent det polære koordinatsystem og definitionen af de trigonometriske funktioner sin og cos. Det er indlysende, at det ved hjælp af disse funktioner er muligt at beskrive placeringen af ethvert punkt på flyet. For at gøre dette er det nok at kende længden af polarstrålen og hældningsvinklen til den reelle akse.
Definition. En indtastning af formen ∣z ∣ ganget med summen af de trigonometriske funktioner cos(ϴ) og den imaginære del i ×sin(ϴ) kaldes et trigonometrisk komplekst tal. Her er betegnelsen hældningsvinklen til den reelle akse
ϴ=arg(z) og r=∣z∣, strålelængde.
Fra definitionen og egenskaberne for trigonometriske funktioner følger en meget vigtig Moivre-formel:
zn =r × (cos(n × ϴ) + i × sin(n × ϴ)).
Ved at bruge denne formel er det praktisk at løse mange ligningssystemer, der indeholder trigonometriske funktioner. Især når problemet med at hæve til en magt opstår.
Modul og fase
For at fuldende beskrivelsen af et komplekst sæt foreslår vi to vigtige definitioner.
Ved at kende Pythagoras sætning er det let at beregne længden af strålen i det polære koordinatsystem.
r=∣z∣=√(x2 + y2), en sådan notation på et komplekst rum kaldes en " modul" og karakteriserer afstanden fra 0 til et punkt på flyet.
Hængningsvinklen af den komplekse stråle til den reelle linje ϴ kaldes almindeligvis fasen.
Definitionen viser, at de reelle og imaginære dele er beskrevet ved hjælp af cykliske funktioner. Nemlig:
- x=r × cos(ϴ);
- y=r × sin(ϴ);
Omvendt er fasen relateret til algebraiske værdier gennem formlen:
ϴ=arctan(x / y) + µ, korrektion µ introduceres for at tage højde for periodiciteten af geometriske funktioner.
Euler-formel
Matematikere bruger ofte den eksponentielle form. Komplekse plantal skrives som udtryk
z=r × ei×ϴ , som følger af Euler-formlen.

Denne post er meget brugt til praktisk beregning af fysiske mængder. Præsentationsform i formulareneksponentielle komplekse tal er særligt praktiske til tekniske beregninger, hvor det bliver nødvendigt at beregne kredsløb med sinusformede strømme, og det er nødvendigt at kende værdien af integraler af funktioner med en given periode. Beregningerne i sig selv tjener som et værktøj i design af forskellige maskiner og mekanismer.
Definer operationer
Som allerede nævnt gælder alle algebraiske love for at arbejde med grundlæggende matematiske funktioner for komplekse tal.
Sumoperation
Når der tilføjes komplekse værdier, tilføjes deres reelle og imaginære dele også.
z=z1 + z2 hvor z1 og z2 - generelle komplekse tal. Ved at transformere udtrykket, efter at have åbnet parenteserne og forenklet notationen, får vi det reelle argument x=(x1 + x2), det imaginære argument y=(y 1 + y2).
På grafen ligner det tilføjelsen af to vektorer ifølge den velkendte parallelogram-regel.
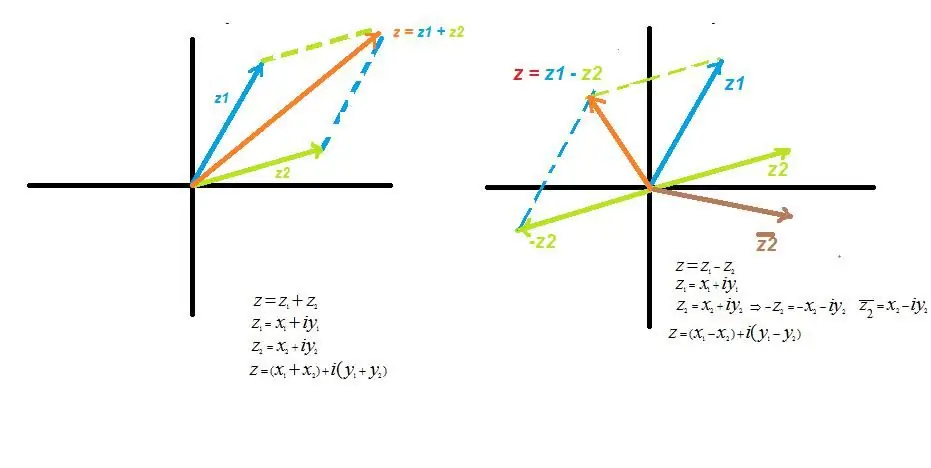
Subtraktionsoperation
Betragtes som et særligt tilfælde af addition, når et tal er positivt, er det andet negativt, dvs. placeret i spejlkvarteret. Algebraisk notation ligner forskellen mellem reelle og imaginære dele.
z=z1 - z2, eller, under hensyntagen til værdierne af argumenterne, på samme måde som tilføjelsen operation, får vi for de reelle værdier x=(x1 - x2) og imaginære y=(y1- y2).
Multiplikation på det komplekse plan
Ved at bruge reglerne for at arbejde med polynomier udleder vi formlenat løse komplekse tal.
Følg de generelle algebraiske regler z=z1×z2, beskriv hvert argument og angiv lignende. De virkelige og imaginære dele kan skrives sådan:
- x=x1 × x2 - y1 × y2,
- y=x1 × y2 + x2 × y 1.
Det ser smukkere ud, hvis vi bruger eksponentielle komplekse tal.
Udtrykket ser således ud: z=z1 × z2 =r1 × eiϴ1 × r2 × eiϴ2=r1 × r2 × ei(ϴ1+ϴ2).
Ydermere bliver modulerne multipliceret, og faserne tilføjes.
Division
Når vi betragter operationen af division som invers af multiplikation, får vi et simpelt udtryk i eksponentiel notation. At dividere værdien z1 med z2 er resultatet af at dividere deres moduler og faseforskel. Formelt, når man bruger den eksponentielle form af komplekse tal, ser det sådan ud:
z=z1 / z2 =r1 × e iϴ1 / r2 × ei ϴ2=r1 / r2× ei(ϴ1-ϴ 2).
I form af algebraisk notation er operationen med at dividere tallene i det komplekse plan skrevet lidt mere kompliceret:
z=z1 / z2.
Beskriver argumenter og udfører polynomietransformationer, det er nemt at få værdierx=x1 × x2 + y1 × y2, henholdsvis y=x2 × y1 - x1 × y2 , men inden for det beskrevne rum giver dette udtryk mening, hvis z2 ≠ 0.
Udtræk roden
Alt ovenstående kan anvendes, når man definerer mere komplekse algebraiske funktioner - hæve til en hvilken som helst potens og omvendt til det - udtrækning af roden.
Ved at bruge det generelle koncept om at hæve til potensen n får vi definitionen:
zn =(r × eiϴ).
Ved brug af almindelige egenskaber, omskriv som:
zn =rn × eiϴ.
Vi har en simpel formel til at hæve et komplekst tal til en potens.
Fra definitionen af graden får vi en meget vigtig konsekvens. En lige potens af den imaginære enhed er altid 1. Enhver ulige potens af den imaginære enhed er altid -1.
Lad os nu studere den inverse funktion - udtræk af roden.
For at lette notationen, lad os tage n=2. Kvadratroden w af den komplekse værdi z på den komplekse plan C anses for at være udtrykket z=±, gyldigt for ethvert reelt argument større end eller lig med nul. For w ≦ 0 er der ingen løsning.
Lad os se på den enkleste andengradsligning z2 =1. Brug komplekse talformler til at omskrive r2 × ei2ϴ =r2 × ei2ϴ=ei0. Det kan ses fra posten, at r2 =1 og ϴ=0, derfor har vi en unik løsning lig med 1. Men dette er i modstrid med forestillingen om, at z=-1 også passer til definitionen af en kvadratrod.
Lad os finde ud af, hvad vi ikke tager højde for. Hvis vi husker den trigonometriske notation, genopretter vi udsagnet - med en periodisk ændring i fasen ϴ ændres det komplekse tal ikke. Lad p angive værdien af perioden, så har vi r2 × ei2ϴ =ei(0+p), hvorfra 2ϴ=0 + p, eller ϴ=p / 2. Derfor, ei0 =1 og eip/2 =-1. Vi fik den anden løsning, som svarer til den generelle forståelse af kvadratroden.
Så for at finde en vilkårlig rod af et komplekst tal, vil vi følge proceduren.
- Skriv den eksponentielle form w=∣w∣ × ei(arg (w) + pk), k er et vilkårligt heltal.
- Det ønskede tal er også repræsenteret i Euler-formen z=r × eiϴ.
- Brug den generelle definition af rodekstraktionsfunktionen r ei ϴ =∣w∣ × ei(arg(w) + pk).
- Fra de generelle egenskaber for ligheden af moduler og argumenter skriver vi rn =∣w∣ og nϴ=arg (w) + p×k.
- Den sidste post af roden af et komplekst tal er beskrevet ved formlen z=√∣w∣ × ei ( arg (w) + pk ) / .
- Bemærk. Værdien af ∣w∣, per definition,er et positivt reelt tal, så roden af enhver grad giver mening.
Felt og konjugation
Afslutningsvis giver vi to vigtige definitioner, der er af ringe betydning for løsning af anvendte problemer med komplekse tal, men som er essentielle for den videre udvikling af matematisk teori.
Udtrykkene for addition og multiplikation siges at danne et felt, hvis de opfylder aksiomerne for et hvilket som helst element i den komplekse plan z:
- Den komplekse sum ændrer sig ikke fra skiftende steder med komplekse termer.
- Sætningen er sand - i et komplekst udtryk kan enhver sum af to tal erstattes af deres værdi.
- Der er en neutral værdi 0, for hvilken z + 0=0 + z=z er sand.
- For ethvert z er der en modsætning - z, hvortil tilføjelse giver nul.
- Når der skiftes sted for komplekse faktorer, ændres det komplekse produkt ikke.
- Multiplikationen af to vilkårlige tal kan erstattes af deres værdi.
- Der er en neutral værdi 1, multiplikation med som ikke ændrer det komplekse tal.
- For hver z ≠ 0 er der en invers af z-1, som ganges med 1.
- At gange summen af to tal med en tredjedel svarer til operationen med at gange hver af dem med dette tal og tilføje resultaterne.
- 0 ≠ 1.
Tallene z1 =x + i×y og z2 =x - i×y kaldes konjugeret.
Sætning. For bøjning er udsagnet sandt:
- Bøjningen af summen er lig med summen af konjugerede elementer.
- Konjugatet af produktet erprodukt af konjugationer.
- Bøjningen af konjugation er lig med selve tallet.
Generelt algebra kaldes sådanne egenskaber feltautomorfismer.
Eksempler
Ved at følge de givne regler og formler for komplekse tal, kan du nemt arbejde med dem.
Lad os overveje de enkleste eksempler.
Opgave 1. Brug ligningen 3y +5 x i=15 - 7i, bestem x og y.
Beslutning. Husk på definitionen af komplekse ligheder, så er 3y=15, 5x=-7. Derfor er x=-7 / 5, y=5.
Opgave 2. Beregn værdierne 2 + i28 og 1 + i135.
Beslutning. Det er klart, at 28 er et lige tal, fra konsekvensen af definitionen af et komplekst tal i potensen har vi i28 =1, hvilket betyder, at udtrykket 2 + i 28 =3. Den anden værdi, i135 =-1, derefter 1 + i135 =0.
Opgave 3. Beregn produktet af værdierne 2 + 5i og 4 + 3i.
Beslutning. Fra de generelle egenskaber ved multiplikation af komplekse tal får vi (2 + 5i)X(4 + 3i)=8 - 15 + i(6 + 20). Den nye værdi vil være -7 + 26i.
Opgave 4. Beregn rødderne af ligningen z3 =-i.
Beslutning. Der er flere måder at finde et komplekst tal på. Lad os overveje en af de mulige. Per definition, ∣ - i∣=1, er fasen for -i -p / 4. Den oprindelige ligning kan omskrives som r3ei3ϴ =e-p/4+pk, hvorfra z=e-p / 12 + pk/3, for ethvert heltal k.
Løsningssættet har formen (e-ip/12,eip/4, ei2 p/3).
Hvorfor har vi brug for komplekse tal
Historien kender mange eksempler, hvor videnskabsmænd, der arbejder på en teori, ikke engang tænker på den praktiske anvendelse af deres resultater. Matematik er først og fremmest et sindets spil, en streng overholdelse af årsag-virkning-forhold. Næsten alle matematiske konstruktioner er reduceret til at løse integral- og differentialligninger, og dem løses til gengæld med en vis tilnærmelse ved at finde rødderne til polynomier. Her støder vi først på paradokset med imaginære tal.
Videnskabelige naturforskere, der løser fuldstændig praktiske problemer, ty til løsninger af forskellige ligninger, opdager matematiske paradokser. Fortolkningen af disse paradokser fører til helt fantastiske opdagelser. Den dobbelte natur af elektromagnetiske bølger er et sådant eksempel. Komplekse tal spiller en afgørende rolle for at forstå deres egenskaber.
Dette har til gengæld fundet praktisk anvendelse inden for optik, radioelektronik, energi og mange andre teknologiske områder. Et andet eksempel, meget sværere at forstå fysiske fænomener. Antistof blev forudsagt på spidsen af en kuglepen. Og kun mange år senere begynder forsøg på at syntetisere det fysisk.
Tro ikke, at der kun er sådanne situationer i fysik. Ikke mindre interessante opdagelser er gjort i dyrelivet, i syntesen af makromolekyler, under studiet af kunstig intelligens. Og det er alt sammen takket væreudvidelse af vores bevidsthed, bevæger os væk fra simpel addition og subtraktion af naturlige værdier.






