Når peer review, for eksempel vurderer produkters konkurrenceevne, er det nødvendigt, som i ethvert videnskabeligt arbejde, at udføre statistisk databehandling. Sidstnævnte begynder med at bestemme konsistensen af ekspertudtalelser, hvis numeriske udtryk er konkordanskoefficienten.
Hvorfor har vi brug for en ekspertkonsensusvurdering?
Denne vurdering er først og fremmest nødvendig, fordi eksperternes meninger kan variere meget om de estimerede parametre. I første omgang udføres vurderingen ved at rangordne indikatorerne og tildele dem en vis betydningskoefficient (vægt). En inkonsistent rangering resulterer i, at disse koefficienter er statistisk upålidelige. Udtalelser fra eksperter med deres krævede antal (mere end 7-10) bør distribueres i henhold til den normale lovgivning.
Begrebet overensstemmelseskoefficient
Så. Konsistens er konkordans. Koefficienten er en dimensionsløs størrelse, der viser forholdet mellem dispersionen og den maksimale spredning i det generelle tilfælde. Lad os generalisere disse begreber.
Konkordansskoefficient er et tal fra 0 til 1, der viser konsistensen af ekspertudtalelser, nårrangordne nogle ejendomme. Jo tættere denne værdi er på 0, jo lavere bliver konsistensen betragtet. Hvis værdien af denne koefficient er mindre end 0,3, anses eksperternes udtalelser for at være inkonsekvente. Når værdien af koefficienten er i området fra 0,3 til 0,7, betragtes konsistensen som gennemsnitlig. En værdi større end 0,7 betragtes som høj konsistens.
Use cases
Når der udføres statistisk forskning, kan der opstå situationer, hvor et objekt ikke kan karakteriseres af to sekvenser, som er statistisk behandlet ved hjælp af konkordanskoefficienten, men af flere sekvenser, som i overensstemmelse hermed rangeres af eksperter med samme niveau af professionalisme på et bestemt område.
Konsistensen af rangeringen udført af eksperter skal bestemmes for at bekræfte rigtigheden af hypotesen om, at eksperter foretager relativt nøjagtige målinger, hvilket tillader dannelsen af forskellige grupperinger i ekspertgrupper, som i vid udstrækning er bestemt af menneskelige faktorer, primært såsom forskelle i synspunkter, koncepter, forskellige videnskabelige skoler, arten af professionel aktivitet osv.
Kort beskrivelse af rangeringsmetoden. Dens fordele og ulemper
Ved rangering bruges rangeringsmetoden. Dens essens ligger i det faktum, at hver egenskab ved objektet er tildelt sin egen specifikke rang. Desuden er hver ekspert, der indgår i ekspertgruppen, denne rang tildeltuafhængigt, hvilket resulterer i behovet for at behandle disse data for at identificere sammenhængen i ekspertudtalelser. Denne proces udføres ved at beregne overensstemmelseskoefficienten.
Den største fordel ved rangeringsmetoden er dens lette implementering.
De største ulemper ved metoden er:
- et lille antal rangordnede objekter, da når deres antal overstiger 15-20, bliver det vanskeligt at tildele objektive rangeringsscore;
- Baseret på brugen af denne metode forbliver spørgsmålet om, hvor langt de undersøgte objekter er fra hinanden i betydning, åbent.
Når du bruger denne metode, skal det tages i betragtning, at vurderingerne er baseret på en form for sandsynlighedsmodel, så de skal anvendes med forsigtighed i betragtning af omfanget.
Kendall's Concordance Rank Coefficient
Bruges til at bestemme forholdet mellem kvantitative og kvalitative træk, der karakteriserer homogene objekter og rangeret efter samme princip.
Denne koefficient bestemmes af formlen:
t=2S/(n(n-1)), hvor
S - summen af forskellene mellem antallet af sekvenser og antallet af inversioner på det andet element;
n - antal observationer.

Beregningsalgoritme:
- X-værdierne er rangeret i stigende eller faldende rækkefølge.
- Y-værdierne er arrangeret i den rækkefølge, de svarer til x-værdierne.
- For hver efterfølgende rangering af y skal du bestemme, hvor mange højere rangværdier der følger den. De lægges sammen, og målet for korrespondance af rækkefølger i x og y beregnes.
- På samme måde beregnes antallet af rækker af y med lavere værdier, som også summeres.
- Tilføj antallet af rækker med højere værdier og antallet af rækker med lavere værdier, hvilket resulterer i værdien S.
Denne koefficient viser forholdet mellem to variable, og kaldes i de fleste tilfælde Kendalls rangkorrelationskoefficient. En sådan afhængighed kan repræsenteres grafisk.
Bestemmelse af koefficient
Hvordan gøres det? Hvis antallet af rangerede træk eller faktorer overstiger 2, bruges konkordanskoefficienten, som i det væsentlige er en multipel variant af rangkorrelation.
Vær forsigtig. Beregningen af konkordanskoefficienten er baseret på forholdet mellem afvigelsen af summen af kvadrater af rækker fra den gennemsnitlige sum af kvadrater af rækker, ganget med 12, til kvadratet af eksperter, ganget med forskellen mellem terningen af tallet af objekter og antallet af objekter.
Beregningsalgoritme
For at forstå, hvor tallet 12 kommer fra i tælleren i beregningsformlen, lad os se på bestemmelsesalgoritmen.
For hver linje med en bestemt eksperts rækker beregnes summen af rækkerne, som er en tilfældig værdi.
Konkordanskoefficienten er generelt defineret som forholdet mellem variansestimatet (D) og den maksimale værdi af variansestimatet(Dmax). Lad os successivt formulere definitionerne af disse mængder.
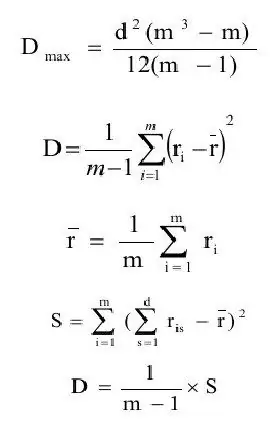
hvor ravg - forventningsestimat;
m - antal objekter.
Ved at erstatte de resulterende formler i forhold til D til Dmax får vi den endelige formel for konkordanskoefficienten:
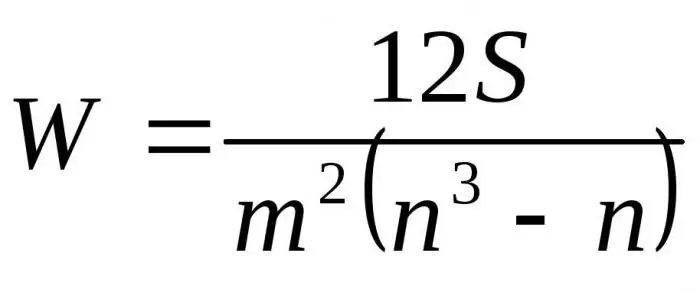
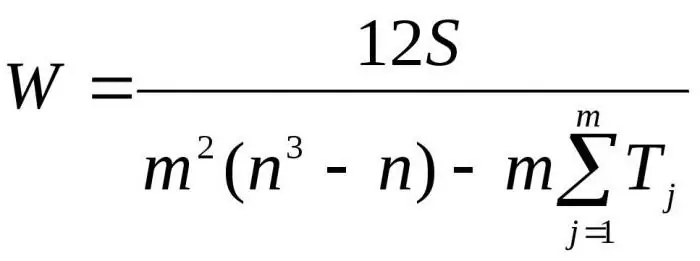
Her er m antallet af eksperter, n er antallet af objekter.
Den første formel bruges til at bestemme konkordansfaktoren, hvis der ikke er nogen relaterede rækker. Den anden formel bruges, hvis der er relaterede rækker.
Så, beregningen af konkordanskoefficienten er slut. Hvad er det næste? Den opnåede værdi evalueres for signifikans ved hjælp af Pearson-koefficienten ved at gange denne koefficient med antallet af eksperter og med antallet af frihedsgrader (m-1). Det resulterende kriterium sammenlignes med tabelværdien, og hvis værdien af den første overstiger den sidste, taler de om betydningen af den undersøgte koefficient.
I tilfælde af relaterede rækker bliver beregningen af Pearson-kriteriet noget mere kompliceret og udføres med følgende forhold: (12S)/(d(m2+ m)-(1/(m-1))x(Ts1 +Ts2 +Tsn)
Eksempel
Antag, at ekspertmetoden vurderer konkurrenceevnen af smør, der sælges i et detailnetværk. Lad os give et eksempel på beregning af konkordanskoefficienten. Før man vurderer konkurrenceevnen, er det nødvendigt at rangere forbrugerenegenskaber ved dette produkt, der er involveret i evalueringen. Lad os antage, at disse egenskaber vil være følgende: smag og lugt, konsistens og udseende, farve, emballage og mærkning, fedtindhold, handelsnavn, producent, pris.
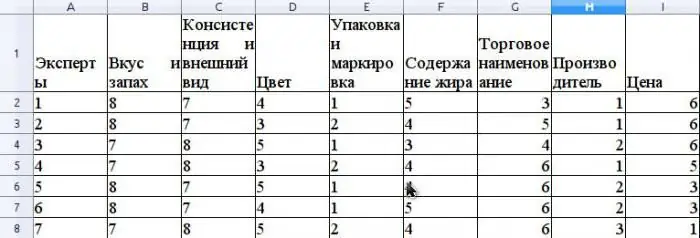
Antag, at ekspertgruppen består af 7 eksperter. Figuren viser resultaterne af rangeringen af disse ejendomme.
Den gennemsnitlige værdi af r beregnes som det aritmetiske gennemsnit og vil være 31,5. For at finde S skal du summere de kvadrerede forskelle mellem ris og r gennemsnit ifølge formlen ovenfor, og bestem, at værdien af S er 1718.
Beregn konkordanskoefficienten ved hjælp af formlen uden at bruge relaterede rækker (rækker ville være relateret, hvis den samme ekspertrådgiver havde de samme rækker for forskellige egenskaber).
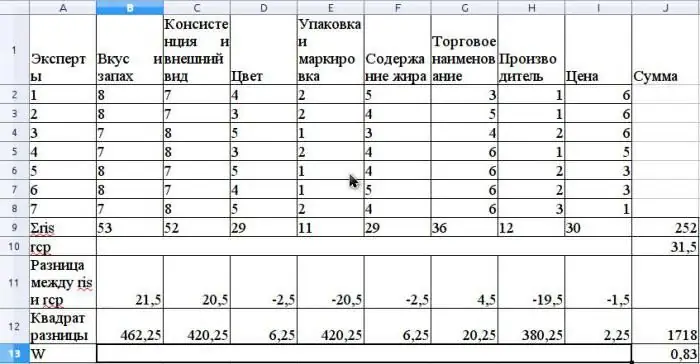
Værdien af denne koefficient vil være 0,83. Dette indikerer en stærk konsensus blandt eksperter.
Tjek dens betydning ved hjælp af Pearson-testen:
7 x 0,83 x (8-1)=40,7.
Pearsons tabelformede test ved 1 % signifikansniveau er 18,5 og ved 5 % - 14,1..
Eksemplet demonstrerer enkelheden og tilgængeligheden af beregningen for enhver person, der kender det grundlæggende i matematiske beregninger. For at lindre dem,brug regnearksformularer.
Afslutningsvis
Således viser overensstemmelseskoefficienten konsistensen af adskillige eksperters udtalelser. Jo længere det er fra 0 og tættere på 1, jo mere konsekvente meninger. Disse koefficienter skal bekræftes ved at beregne Pearson-kriteriet.






