I fysik studeres emnet parallel- og serieforbindelse, og det kan ikke kun være ledere, men også kondensatorer. Det er vigtigt her ikke at blive forvirret over, hvordan hver af dem ser ud på diagrammet. Og kun derefter anvende specifikke formler. Du skal i øvrigt huske dem udenad.
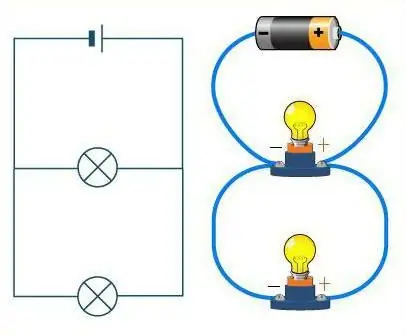
Hvordan skelner man mellem disse to forbindelser?
Tag et nærmere kig på diagrammet. Hvis ledningerne er repræsenteret som en vej, vil bilerne på den spille rollen som modstande. På en lige vej uden gafler kører biler efter hinanden i en kæde. Serieforbindelsen af ledere ser også ens ud. Vejen kan i dette tilfælde have et ubegrænset antal sving, men ikke et enkelt kryds. Uanset hvordan vejen (ledningerne) vippede, vil maskinerne (modstandene) altid være placeret efter hinanden, i én kæde.
Det er en helt anden sag, hvis en parallelforbindelse overvejes. Så kan modstandene sammenlignes med atleter i starten. De erstår hver på sit spor, men de har samme bevægelsesretning, og målstregen er på samme sted. På samme måde, modstande - hver af dem har sin egen ledning, men de er alle forbundet på et tidspunkt.
Formler for aktuel styrke
Det diskuteres altid i emnet "Elektricitet". Parallel- og serieforbindelser påvirker mængden af strøm i modstande på forskellige måder. For dem udledes formler, der kan huskes. Men det er nok bare at huske betydningen, der er investeret i dem.
Så strømmen i serieforbindelse af ledere er altid den samme. Det vil sige, i hver af dem er værdien af den nuværende styrke ikke anderledes. Du kan tegne en analogi, hvis du sammenligner en ledning med et rør. I den løber vandet altid på samme måde. Og alle forhindringer på dens vej vil blive fejet væk med samme kraft. Det samme med nuværende. Derfor ser formlen for den samlede strøm i et kredsløb med serieforbindelse af modstande således ud:
I gen=I 1=I 2
Her angiver bogstavet I strømmens styrke. Dette er en almindelig notation, så du skal huske den.
Strøm i parallelforbindelse vil ikke længere være en konstant værdi. Med samme analogi med et rør viser det sig, at vandet vil blive delt i to vandløb, hvis hovedrøret har en gren. Det samme fænomen observeres med strøm, når en forgrening af ledninger vises i dens vej. Formlen for den samlede strømstyrke, når lederne er parallelforbundne:
I gen=I 1 + I 2
Hvis forgreningen består af ledninger, dermere end to, så vil der i ovenstående formel være flere led med det samme tal.
Formler til stress
Når der betragtes et kredsløb, hvor lederne er forbundet i serie, er spændingen i hele sektionen bestemt af summen af disse værdier på hver specifik modstand. Du kan sammenligne denne situation med plader. Det vil være nemt for en person at holde en af dem, han vil også være i stand til at tage den anden i nærheden, men med besvær. En person vil ikke længere være i stand til at holde tre plader ved siden af hinanden, hjælp fra en anden vil være påkrævet. Etc. Folks indsats går op.
Formlen for den samlede spænding af en sektion af et kredsløb med en serieforbindelse af ledere ser sådan ud:
U gen=U 1 + U 2, hvor U er den vedtagne betegnelse for elektrisk spænding.
En anden situation opstår, hvis en parallelforbindelse af modstande overvejes. Når tallerkener stables oven på hinanden, kan de stadig holdes af én person. Så du behøver ikke tilføje noget. Den samme analogi observeres, når lederne er forbundet parallelt. Spændingen på hver af dem er den samme og lig med den, der er på dem alle på én gang. Formlen for samlet spænding er:
U gen=U 1=U 2
Formler for elektrisk modstand
Du kan ikke længere huske dem, men kender formlen for Ohms lov og udleder den ønskede ud fra den. Det følger af denne lov, atspænding er lig med produktet af strøm og modstand. Det vil sige U=IR, hvor R er modstanden.
Så afhænger formlen, du skal arbejde med, af, hvordan lederne er forbundet:
- i serien, så du har brug for lighed for spænding - IgenRtotal=I1R1 + I2R2;
- parallelt er det nødvendigt at bruge formlen for den aktuelle styrke - Utotal / Rtotal=U 1/ R1 + U2 / R2 .
Efterfulgt af simple transformationer, som er baseret på, at i den første lighed har alle strømme den samme værdi, og i den anden - er spændingerne ens. Så de kan forkortes. Det vil sige, at følgende udtryk opnås:
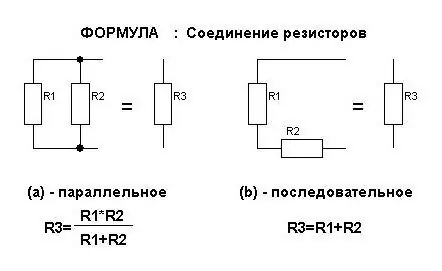
- R gen=R 1 + R 2 (til serieforbindelse af ledere)
- 1 / R gen=1 / R 1 + 1 / R 2(når den er tilsluttet parallelt).
Når antallet af modstande forbundet til netværket stiger, ændres antallet af termer i disse udtryk.
Det er værd at bemærke, at parallel- og serieforbindelse af ledere har en anden effekt på den samlede modstand. Den første af dem reducerer modstanden af kredsløbssektionen. Desuden viser det sig at være mindre end den mindste af de anvendte modstande. Når det er serieforbundet, er alt logisk: værdierne lægges sammen, så det samlede antal vil altid være det største.
Arbejdsaktuelt
De foregående tre størrelser udgør lovene for parallelforbindelse og seriearrangement af ledere i et kredsløb. Derfor er det bydende nødvendigt at kende dem. Om arbejde og magt skal du bare huske den grundlæggende formel. Det er skrevet som følger: A \u003d IUt, hvor A er strømmens arbejde, t er tidspunktet for dens passage gennem lederen
For at bestemme det samlede arbejde med en seriel forbindelse, skal du udskifte spændingen i det originale udtryk. Du får ligheden: A \u003d I(U 1 + U 2)t ved at åbne parenteserne, hvori det viser sig, at arbejde på hele sektionen er lig med beløbet på hver specifik nuværende forbruger.
Ræsonementet forløber på samme måde, hvis en parallel forbindelsesordning overvejes. Kun den nuværende styrke formodes at blive udskiftet. Men resultatet bliver det samme: A=A 1 + A 2.
Nuværende strøm
Når du udleder en formel for effekt (notation "P") af en kredsløbssektion, skal du igen bruge én formel: P \u003d UI. Efter en sådan begrundelse viser det sig, at parallelle og serieforbindelser er beskrevet af sådan en formel for magt: P \u003d P1 + P 2.
Det vil sige, at uanset hvordan ordningerne er udarbejdet, vil den samlede effekt være summen af de involverede i arbejdet. Dette forklarer det faktum, at det er umuligt at inkludere mange kraftfulde enheder i lejlighedsnetværket på samme tid. Hun kan bare ikke klare byrden.
Hvordan påvirker forbindelsen af ledere reparationen af nytårsguirlanden?
Umiddelbart efter at en af pærerne er brændt ud, bliver det klart, hvordan de var forbundet. Påseriel forbindelse, vil ingen af dem lyse. Dette skyldes, at en lampe, der er blevet ubrugelig, skaber et brud i kredsløbet. Derfor skal du tjekke alt for at afgøre, hvilken der er udbrændt, udskifte den - og guirlanden begynder at virke.
Hvis den bruger en parallelforbindelse, holder den ikke op med at virke, hvis en af pærerne svigter. Når alt kommer til alt, vil kæden ikke være helt brudt, men kun en parallel del. For at reparere sådan en guirlande behøver du ikke kontrollere alle kredsløbets elementer, men kun dem, der ikke lyser.
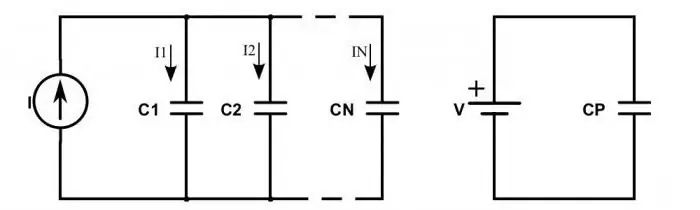
Hvad sker der med et kredsløb, hvis kondensatorer er inkluderet i stedet for modstande?
Når de er forbundet i serie, observeres følgende situation: ladninger fra strømkildens plusser kommer kun til de ydre plader på de ekstreme kondensatorer. Dem i mellem sender simpelthen den ladning langs kæden. Dette forklarer det faktum, at de samme ladninger vises på alle pladerne, men med forskellige fortegn. Derfor kan den elektriske ladning af hver seriekoblet kondensator skrives som følger:
q gen =q 1=q 2.
For at bestemme spændingen på hver kondensator skal du kende formlen: U=q / C. I den er C kondensatorens kapacitans.
Total spænding følger samme lov som modstande. Ved at erstatte spændingen i kapacitansformlen med summen får vi derfor, at enhedernes samlede kapacitans skal beregnes ved hjælp af formlen:
C=q / (U 1 + U2).
Du kan forenkle denne formel ved at vende brøkerne og erstatte forholdet mellem spænding og opladning med kapacitans. Det viser sig følgende lighed: 1 / С=1 / С 1 + 1 / С 2.
Situationen ser noget anderledes ud, når kondensatorerne er parallelkoblet. Derefter bestemmes den samlede ladning af summen af alle ladninger, der akkumuleres på pladerne af alle enheder. Og spændingsværdien bestemmes stadig efter almindelige love. Derfor er formlen for den samlede kapacitans for kondensatorer forbundet parallelt:
С=(q 1 + q 2) / U.
Det vil sige, at denne værdi betragtes som summen af hver af de enheder, der bruges i forbindelsen:
S=S 1 + S 2.
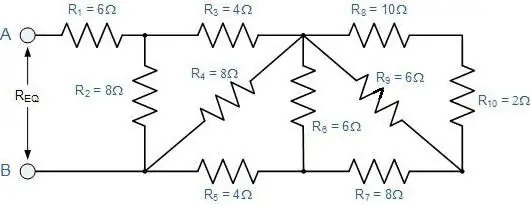
Hvordan bestemmes den samlede modstand af en vilkårlig forbindelse af ledere?
Det vil sige en, hvor successive sektioner erstatter parallelle, og omvendt. For dem er alle de beskrevne love stadig gyldige. Kun du behøver at anvende dem i etaper.
For det første skal det ment alt udvide ordningen. Hvis det er svært at forestille sig det, så skal du tegne, hvad der sker. Forklaringen bliver tydeligere, hvis vi betragter den med et specifikt eksempel (se figur).
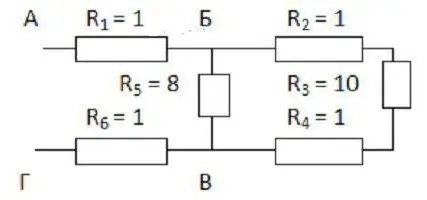
Det er praktisk at begynde at tegne fra punkt B og C. De skal placeres i en vis afstand fra hinanden og fra arkets kanter. Til venstre nærmer en ledning sig punkt B, og to er allerede rettet mod højre. Punkt B har på den anden side to grene til venstre og en ledning efter sig.
Nu skal du udfylde mellemrummet mellem disseprikker. Tre modstande med koefficienter på 2, 3 og 4 skal placeres langs den øverste ledning, og den med et indeks på 5 vil gå fra bunden. De tre første er forbundet i serie. Med den femte modstand er de parallelle.
De resterende to modstande (den første og sjette) er forbundet i serie med den betragtede sektion af BV. Derfor kan tegningen blot suppleres med to rektangler på hver side af de valgte punkter. Det er tilbage at anvende formlerne til at beregne modstanden:
- først den, der blev givet til seriel forbindelse;
- så for parallel;
- og igen i træk.
På denne måde kan du implementere en hvilken som helst, selv meget kompleks ordning.
Problemet med seriel forbindelse af ledere
Tilstand. To lamper og en modstand er forbundet i et kredsløb bag hinanden. Den samlede spænding er 110 V, og strømmen er 12 A. Hvad er værdien af modstanden, hvis hver lampe er normeret til 40 V?
Beslutning. Da en serieforbindelse overvejes, er formlerne for dens love kendte. Du skal blot anvende dem korrekt. Start med at finde ud af spændingsværdien over modstanden. For at gøre dette skal du trække to gange spændingen af en lampe fra totalen. Det viser sig 30 V.
Nu hvor to størrelser er kendt, U og I (den anden af dem er givet i betingelsen, da den samlede strøm er lig med strømmen i hver serieforbruger), kan vi beregne modstanden af modstanden vha. Ohms lov. Det viser sig at være 2,5 ohm.
Svar. Modstandens modstand er 2,5 ohm.
Opgavetil tilslutning af kondensatorer, parallel og serie
Tilstand. Der er tre kondensatorer med kapaciteter på 20, 25 og 30 mikrofarad. Bestem deres samlede kapacitans, når de er forbundet i serie og parallelt.
Beslutning. Det er nemmere at starte med en parallelforbindelse. I denne situation skal alle tre værdier blot tilføjes. Den samlede kapacitans er således 75uF.
Beregningerne bliver noget mere komplicerede, når disse kondensatorer er forbundet i serie. Når alt kommer til alt, skal du først finde forholdet mellem enhed til hver af disse kapaciteter og derefter tilføje dem til hinanden. Det viser sig, at enheden divideret med den samlede kapacitet er 37/300. Så er den ønskede værdi cirka 8 mikrofarads.
Svar. Den samlede kapacitans i serieforbindelse er 8 uF, parallelt - 75 uF.






