Propositionalgebra er en eksakt videnskab, der ikke går på kompromis. For at løse eksempler med konjunktion, disjunktion, implikation og så videre kan du bygge en sandhedstabel i Excel-applikationen. Den er udstyret med et sæt logiske funktioner, der automatiserer og letter processen med at finde resultatet.
Matematisk logik: grundlæggende begreber
Aristoteles betragtes som grundlæggeren af den formelle logik. I det 17. århundrede G. Leibniz foreslog at introducere symboler til at definere udsagn. D. Buhl konsoliderede den erhvervede viden og markerede for første gang sætninger med symboler.
Skematisk erstattes "TRUE" med 1 og "FALSE" med 0.
Under erklæringen forstås enhver deklarativ sætning, der giver enhver information og er i stand til at tage værdien af sandhed eller falskhed. I algebra abstraheres logikker fra den semantiske belastning af sætninger og tager kun hensyn til logiske værdier.
Negation er et nyt udtryk, der tager værdien af sand, hvis det er falsk og omvendt.
Konjunktion af tovariable kaldes en ny sætning, som tager værdien af sandhed i tilfælde af samtidig betegnelse "1" og falskhed i andre situationer.
Disjunktionen af to udsagn forstås som et nyt udtryk, der kun tager værdien "FALSK", hvis der er "0" og "TRUE" i andre variationer på samme tid.
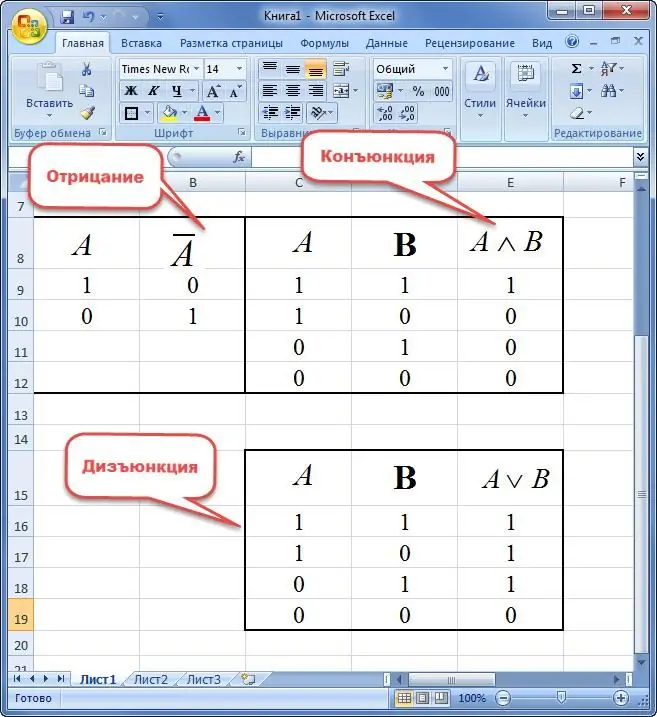
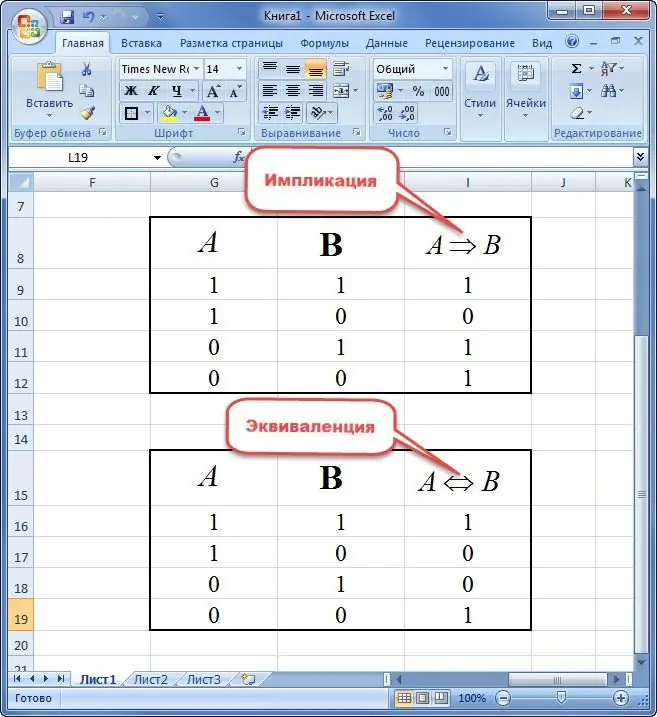
En implikation af to variable er en ny sætning, hvori:
- hvis præmissen er sand, og konsekvensen er falsk, så er udtrykket lig med "0";
- udsagn er lig med "1" i andre tilfælde.
Tilsvarende for to variable forstås som et nyt udsagn, der kun tager værdien af sandhed, hvis elementerne er ens. Ellers er tilbuddet "0".
Logiske værdier af udtryk præsenteres norm alt i tabelform. Der er et andet navn for denne form for information. De siger, at for et udsagn skal du bygge en sandhedstabel. Den specificerer startværdierne for alle variable, og derefter beregnes resultatet af hele udtrykket.
Algorithme til implementering af beregninger i logiske operationer
For at bygge en sandhedstabel skal du kende den rækkefølge, handlingerne udføres i. I et udtryk med flere operander udføres beregningen i følgende rækkefølge:
- inversion (negation);
- konjunktion (logisk funktion i Excel "AND");
- disjunction (boolesk operator i Excel "ELLER");
- implikation (konsekvens);
- ækvivalens.
Der er to operationer mere, men deres prioritet er ikke defineret:
- Schaeffers slagtilfælde;
- Pierce-pil.
Beregningsalgoritmen ændres, hvis udtrykket er omgivet af parenteser.
Rækkefølgen for at konstruere en tabelform for logiske operander i Excel
Før du finder værdien af et udtryk, skal du studere begrebet en logisk algebraformel. Definitionen siger, at dette er et komplekst udtryk, der består af de enkleste udsagn forbundet med logiske operander.
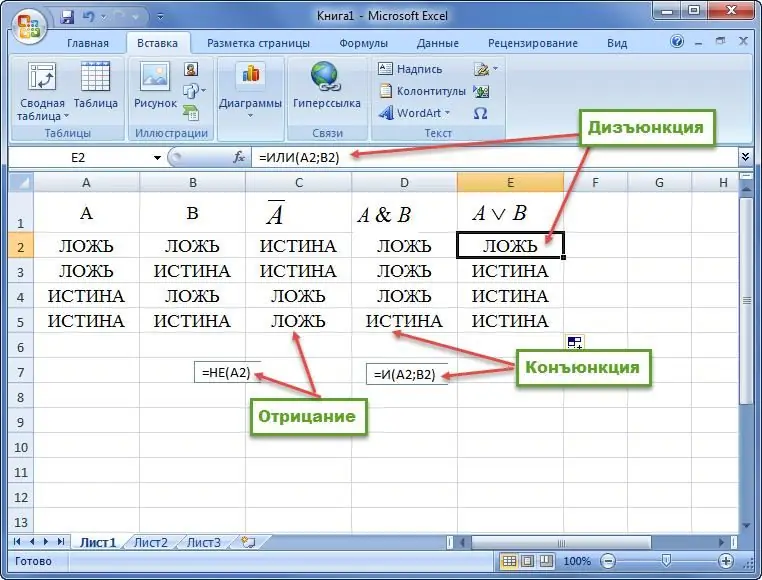
Eksempel 1. Konstruer en sandhedstabel for konjunktion, disjunktion og negation.
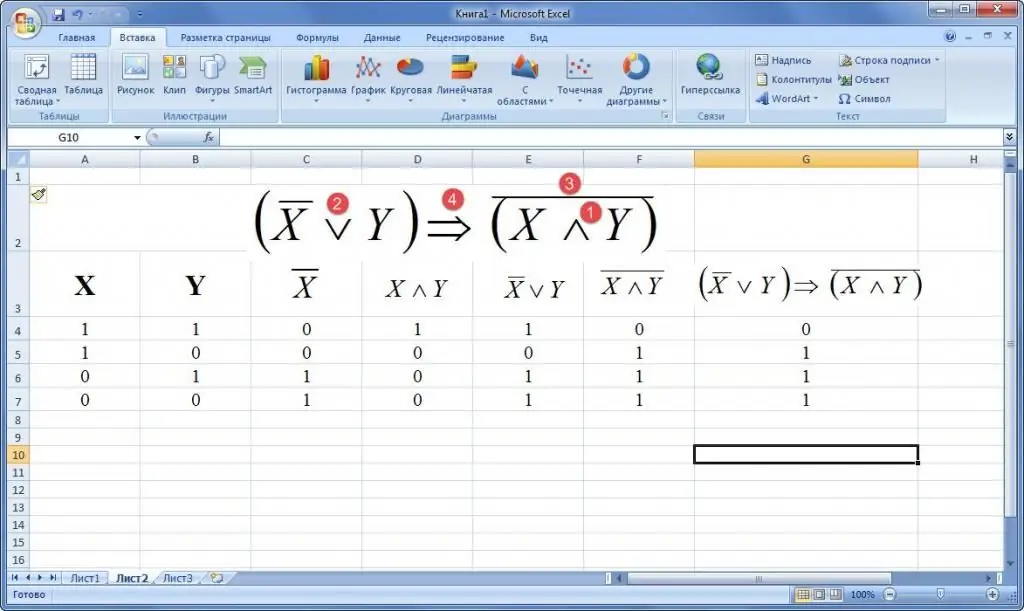
Eksempel 2. Givet en formel for logikkens algebra. Byg en sandhedstabel. Eksempler er givet nedenfor.
Eksempel 3. Hvordan man bygger en sandhedstabel i Excel, givet en formel for logisk algebra i en verbal beskrivelse. Siger: "Hvis en trekant er ligesidet, så er alle dens kanter ens, eller alle dens vinkler er ens."
Først skal du analysere den sammensatte sætning i minimale elementer:
- Den første del af udtrykket: A="ligesidet trekant".
- Second: B="alle sider af figuren er ens".
- Tredje: C="alle vinkler i en trekant er lige store".
Derefter kompileres og løses et udtryk i Excel-softwarepakken.
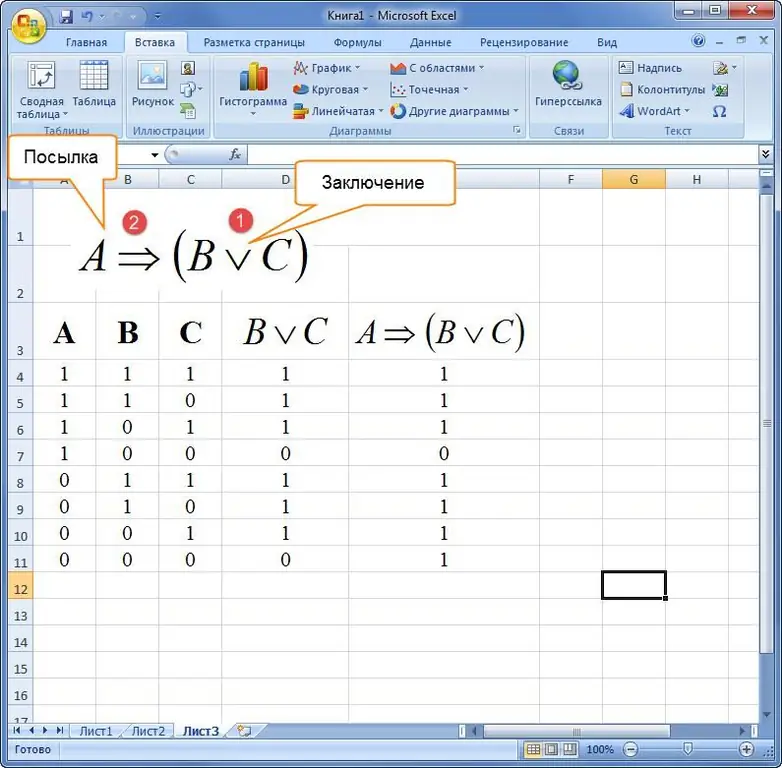
Når du kompilerer sandhedstabeller, er det vigtigt at huske rækkefølgen af operationer.






