Der er regneark, hvor det er nødvendigt at anvende logiske funktioner, logiske skemaer i forskellige rækkefølger. Microsoft Excel-softwarepakken kommer til undsætning. Den kan ikke kun beregne den logiske værdi af et udtryk, men også udføre komplekse matematiske beregninger.
Hvad er Excel?
Et softwareprodukt designet til at fungere med regneark. Skabt af Microsoft og egnet til næsten ethvert operativsystem. Her kan du bruge begge formler til at finde resultater og bygge grafer og diagrammer af forskellige typer.
Brugeren bruger ikke kun logiske funktioner i Excel, men også matematiske, statistiske, økonomiske, tekst osv.
Excel-funktioner
Anvendelsesområderne for softwareproduktet er forskellige:
- Excel-regnearket er et færdiglavet regneark, så det er ikke nødvendigt for brugeren at udføre beregninger for at bringe dokumentet til den korrekte form.
- Softwarepakken tilbyder brug af boolske funktioner samt trigonometriske, statistiske,tekst osv.
- Baseret på beregninger bygger Excel grafer og diagrammer.
- Fordi softwarepakken indeholder et stort bibliotek af matematiske og statistiske funktioner, kan skolebørn og studerende bruge den til at færdiggøre laboratorie- og semesteropgaver.
- Det er nyttigt for brugeren at bruge funktionerne i Excel til hjemme- og personlige beregninger.
- VBA-programmeringssproget er indbygget i softwareproduktet, hvilket kan gøre livet lettere for en revisor, når en lille virksomheds arbejdsgange automatiseres.
- Excel-regnearket fungerer også som en database. Fuld funktionalitet implementeres kun fra 2007-versionen. Tidlige produkter havde en linjegrænse.
- Når du opretter rapporter af forskellig art, kommer Excel til undsætning, da det hjælper med at skabe en pivottabel.
Excel Logical Operators
Booleske udtryk forstås som de data, der er nødvendige for at skrive elementer, hvor konjunktion og disjunktion, såvel som andre operatorer, matcher tal, formler, tekst. Med deres hjælp er beskeden skrevet i symbolsk form, hvilket indikerer handlingen.
Logiske funktioner (ellers kaldet booleske) bruger tal, tekst, links med celleadresser som elementer.
Der er flere måder at lære mere om hver operator og dens syntaks på:
- Call Function Wizard.
- Brug Microsoft-hjælp via F1.
- I 2007-versioner af Excel skal du undersøge sammensætningen af hver kategori på værktøjslinjen.
Boolsk algebra
Grundlæggeren af propositionel logik (et andet navn for et afsnit af matematik) er D. Buhl, som i sin ungdom var engageret i oversættelser af oldgræske filosoffers værker. Det var derfra, han fik viden og foreslog at indføre særlige betegnelser for udsagn: 1 - Sandt, 0 - Falskt.
Boolsk algebra er en gren af matematikken, der studerer udsagn, behandler dem som logiske værdier og udfører operationer på dem. Ethvert udsagn kan kodes og derefter bruges, manipuleres for at bevise sandt eller falsk.
En boolsk funktion kaldes f(x1, x2, …, x ), fra n variable, hvis funktionen eller en af dens operatorer kun tager værdier fra sættet {0;1}. Logikkens algebras love anvendes til at løse problemer, i programmering, kodning osv.
Du kan vise en boolesk funktion på følgende måder:
- verbal (udsagn skrevet i tekstform);
- tabel;
- numeric;
- grafik;
- analytisk;
- koordinat.
Og funktion
AND-operatoren er en forbindelse i Excel-softwarepakken. Ellers kaldes det logisk multiplikation. Det er norm alt angivet med ∧, &,eller tegnet mellem operanderne er helt udeladt. Funktionen er nødvendig for at bestemme rigtigheden af det indtastede udtryk. I boolsk algebra tager en konjunktion værdier fra et sæt, og resultatet af beregningen skrives også til det. Logisk multiplikation sker:
- binær, fordi den indeholder 2operand;
- ternær hvis der er 3 multiplikatorer;
- n-år, hvis sættet indeholder n operander.
Du kan løse et eksempel ved at matche reglen eller ved at oprette en sandhedstabel. Hvis udtrykket indeholder flere operander, er det mere bekvemt at bruge Excel-softwarepakken til den anden løsning, da hele processen vil være besværlig ved manuel beregning.
Resultatet af beregninger kan være:
- True: hvis alle argumenter er sande.
- False: hvis alle kriterier er falske eller mindst et af dem.
Operatorerne "AND" og "OR" kan indeholde op til 30 kriterier.
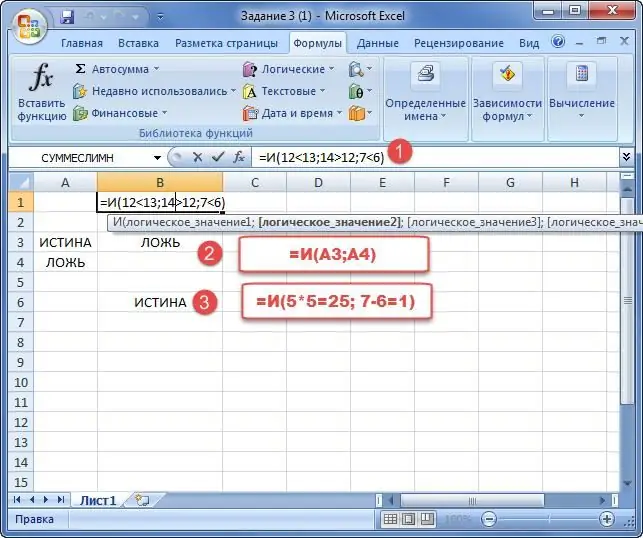
Eksempel.
1) Det er nødvendigt at fastslå sandheden af de indtastede data. Det sidste eksempel i parentes er naturligvis ikke matematisk korrekt, så funktionen vil returnere False.
2) De to celler har modsatte værdier. OG-funktionen returnerer Falsk, fordi et af argumenterne er falsk.
3) Aritmetiske operationer er indstillet. Det er nødvendigt at kontrollere deres sandhed. Denne operator returnerer "True", fordi alt er korrekt ud fra et aritmetisk synspunkt.
Funktion "ELLER"
"ELLER"-operatoren i kategorien "Logiske funktioner" er en disjunktion, dvs. den giver dig mulighed for at få et sandfærdigt svar i en ikke-kategorisk form. Et andet navn for en operator i boolsk algebra: logisk tilføjelse. Angiv: ∨, +, "eller". Variabler tager værdier fra sættet, og svaret er skrevet der.
Resultaterne af beregningerne er:
- True: hvis nogen af eller alle argumenterne er sande.
- False: hvis alle kriterier er falske.
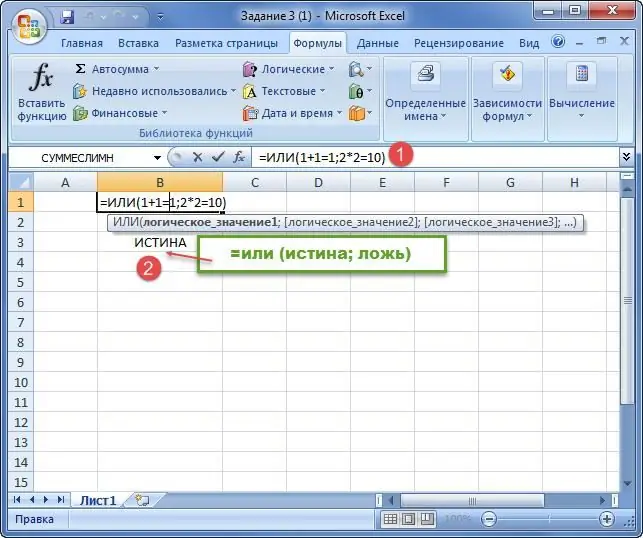
Eksempel.
1) Disjunktion i Excel kontrollerer ikke kun logiske udtryk, men også matematiske for korrekthed. Så i dette særlige tilfælde er begge resultater falske fra et aritmetisk synspunkt, så svaret er falsk.
2) Operatoren returnerer True, fordi et af argumenterne er sandt, og det andet er falsk. Dette er et gyldigt kriterium for disjunktion.
IF-funktion
I gruppen "Logiske funktioner" indtager "IF"-operatøren en ære. Funktionen er nødvendig for at få et resultat, hvis oplysningerne er sande, og et andet resultat, hvis dataene er falske.
- I en betinget erklæring er det muligt at kontrollere op til 64 betingelser ad gangen.
- Hvis et af kriterierne er en matrix, kontrollerer funktionen hvert element.
- Hvis svaret er falsk, men formlen ikke specificerer, hvad totalen skal være i tilfælde af "False", giver operatoren et resultat lig med 0.
Eksempel.
Given:
- produktnavn;
- dens pris for 1 enhed;
- antal købte varer;
- pris.
Det er nødvendigt at beregne kolonnen "Betales". Hvis købsprisen overstiger 1000 rubler, får køberen 3% rabat. Ellers er kolonnerne "TOTAL" og "Betales" de samme.
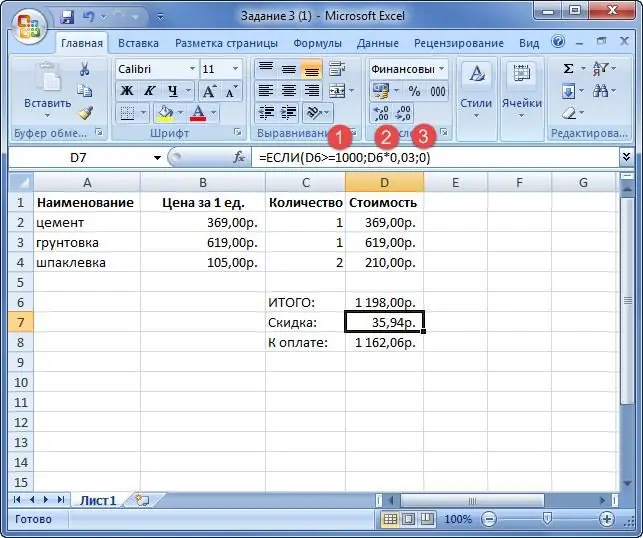
1) Tilstandstjek: prisen overstiger 1000 rubler.
2) Hvis det er sandtkriterieomkostninger ganges med 3%.
3) Hvis erklæringen er falsk, afviger resultatet "Betales" ikke fra "TOTAL".
Tjekker flere betingelser
Der er en tabel, der viser karaktererne for eksamen og lærerens karakter.
1) Det er nødvendigt at kontrollere, om den samlede score er mindre end 35. Hvis svaret er sandt, er resultatet af arbejdet "Failed."
2) Hvis den forrige betingelse er falsk, er scoren >35, operatøren fortsætter til næste argument. Hvis værdien i cellen er >=75, tildeles "Fremragende" ved siden af den. Ellers vil funktionen returnere "Bestået".
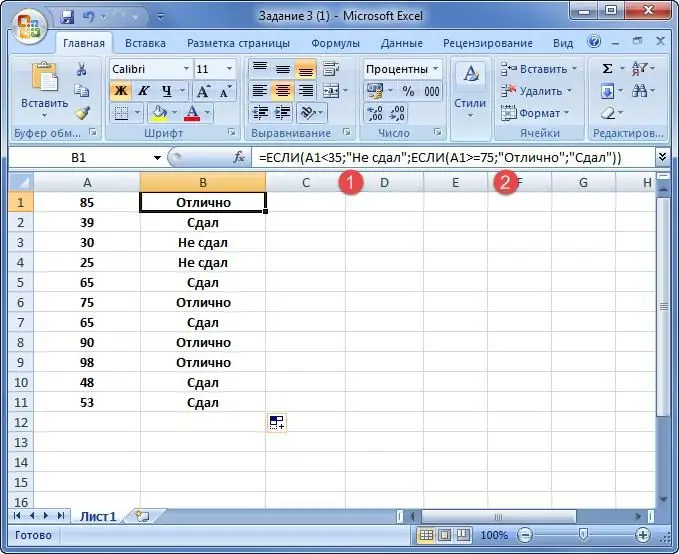
Selvom "If"-operatoren arbejder med booleske værdier, fungerer den også fint med tal.
Eksempel.
Data:
- leverandørnavne;
- deres salg.
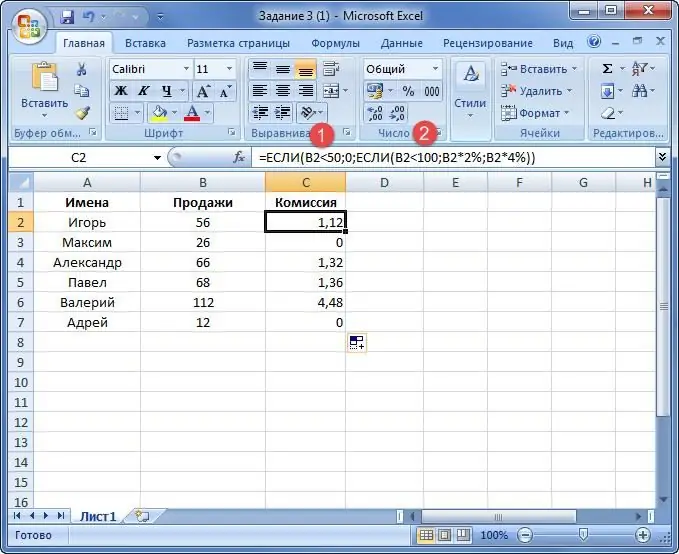
Det skal beregnes, hvilken af sælgerne, hvilken provision der skal betales:
- hvis antallet af salg er mindre end 50 tusind, opkræves procentdelen ikke;
- hvis mængden af transaktioner varierer mellem 50-100 tusind, så er provisionen 2 %;
- hvis antallet af salg er mere end 100.000, så udstedes bonussen i et beløb på 4%.
Under tallet 1 er den første blok "IF", hvor den kontrolleres for sandhed. Hvis betingelsen er falsk, udføres blok 2, hvor yderligere 2 kriterier tilføjes.
Funktionen "IFERROR"
Booleske funktioner suppleres af denne operator, fordi den er i stand til at returnere et resultat, hvis der er en fejl i formlen. Jeg faldersandt, "IFERROR" returnerer resultatet af beregningen.
Funktionen "TRUE" og "FALSE"
Booleske funktioner i Excel kan ikke undvære operatoren "TRUE". Det returnerer den tilsvarende værdi.
Det omvendte af "TRUE" er "FALSE". Begge funktioner tager ingen argumenter og bruges sjældent som selvstændige eksempler.
NOT operator
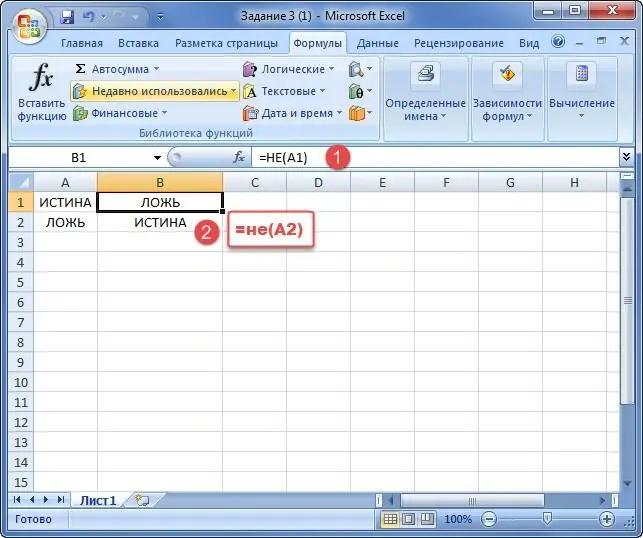
Alle logiske funktioner i Excel kan afvises ved at bruge "NOT"-operatoren. Den værdi, der indtastes ved brug af denne procedure, vil resultere i det modsatte.
Eksempel.
Det er klart, at operatøren giver det modsatte svar til de originale data.
Minimering af logiske funktioner
Dette fænomen er direkte relateret til oprettelsen af et kredsløb eller et kredsløb. Dette kommer til udtryk gennem dets kompleksitet og omkostninger, proportionaliteten af antallet af logiske operationer og antallet af forekomster af argumenter. Hvis du bruger logikkens aksiomer og sætninger, kan du forenkle funktionen.
Der er specielle algoritmiske minimeringsmetoder. Takket være dem er brugeren i stand til selvstændigt at forenkle funktionen hurtigt og uden fejl. Blandt disse metoder er:
- Carnot-kort;
- Quine-metoden;
- implikant matrixalgoritme;
- Quine-McCluskey-metode osv.
Hvis antallet af argumenter ikke overstiger 6, så er det bedre for brugeren at bruge Karnot-kortmetoden for klarheden. Ellers anvendes Quine-McCluskey-algoritmen.






