I matematik er summering (angivet med det store græske sigma-symbol) et sæt summer af tal. Hvad er beløbet? Dette er resultatet af en sådan handling. Hvis tallene lægges til efter hinanden fra venstre mod højre, er mellemresultatet en delsum.
Hvad er beløbet?
De tal, der skal summeres, kan være heltal, rationelle, reelle eller komplekse. Ud over dem kan andre typer værdier tilføjes: vektorer, matricer, polynomier og generelt elementer af enhver additiv gruppe (eller endda en monoid).
Hvis antallet af elementer i vilkårene er endeligt, giver summeringen altid en veldefineret værdi. Summeringen af en uendelig række af værdier kaldes en serie. Dens værdi kan ofte bestemmes ved hjælp af en grænse (selv om værdien nogle gange kan være uendelig).
Sequences
Summeringen af tal [3, 7, 2, 1] kan defineres ved et udtryk, hvis værdi er summen af de cifre, der er inkluderet i det, for eksempel 3 + 7 + 2 + 1=13. Da tilføjelseassociativt afhænger summen ikke af, hvordan termerne er grupperet, f.eks. (3 + 7) + (2 + 1) og 3 + ((7 + 2) + 1) er begge lig med ni, så parenteser undværes norm alt. Addition er også kommutativ, så omarrangering af vilkårene ændrer ikke værdien af summen. Bemærk, at denne egenskab muligvis ikke fungerer for uendelig summering.

Der er ingen speciel notation for summering af sekvenser af denne art. Der er kun en lille nuance, hvis der er mindre end to elementer. Summeringen af en sekvens af et medlem indeholder ikke et plustegn (det kan ikke skelnes fra formen af selve tallet), og hvis der slet ikke er nogen elementer, kan det ikke engang skrives (men i stedet kan det betegnes med dens værdi "0"). Hvis sekvensens vilkår er specificeret af et specifikt mønster, såsom en funktion, så kan summeringsoperatoren være nyttig eller endog væsentlig.
Record
For at forstå, hvad en sum er, er det også nødvendigt at analysere dens udseende.
For at summere en sekvens af heltal fra 1 til 100 bruges ofte et udtryk, der inkluderer en ellipse for at angive de manglende medlemmer: 1 + 2 + 3 + 4 + … + 99 + 100. Mønsteret er ret let at se i dette eksempel. For mere komplekse muligheder er det dog nødvendigt at specificere nøjagtigt den regel, der bruges til at finde værdien af elementerne, hvilket kan opnås ved hjælp af "Σ" summeringsoperatoren. Ved at bruge dette symbol (sigma) kan du anvende følgende notation:
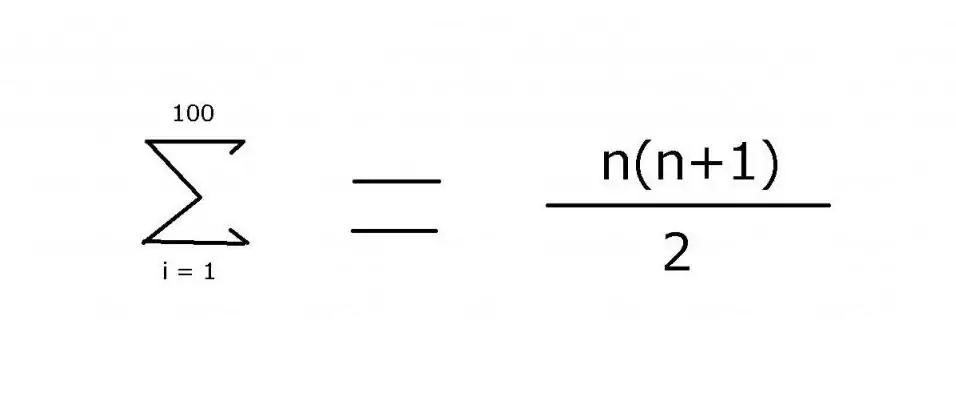
Værdien af dette udtryk er 5050. Det kan findes ved hjælp af matematisk induktion, som er hvor anden del af formlen kom fra.
For forskellige sekvenser vil formlen ændre sig. Optagelsesprocessen reduceres til at søge efter forbilledet af en uendelig sekvens og derefter beskrive det med en formel. Efter at have gjort dette, er det ikke svært at forstå, hvad beløbet er i en bestemt sag.
Når det er nødvendigt at præcisere, at tal lægges sammen med deres fortegn (plus eller minus), bruges udtrykket algebraisk sum. I elektrisk kredsløbsteori betragter Kirchhoffs kredsløbslove f.eks. den algebraiske sum af strømme i et netværk af ledere, der mødes i et punkt, hvilket giver modsatte tegn til strømme, der flyder ind og ud af en knude.






