Elasticitetsmodul er en fysisk størrelse, der karakteriserer et materiales elastiske opførsel, når en ekstern kraft påføres det i en bestemt retning. Et materiales elastiske opførsel betyder dets deformation i det elastiske område.
Historie om studiet af materialers elasticitet

Den fysiske teori om elastiske kroppe og deres adfærd under påvirkning af ydre kræfter blev overvejet i detaljer og studeret af den engelske videnskabsmand fra det 19. århundrede, Thomas Young. Selve begrebet elasticitet blev imidlertid udviklet tilbage i 1727 af den schweiziske matematiker, fysiker og filosof Leonhard Euler, og de første eksperimenter relateret til elasticitetsmodulet blev udført i 1782, altså 25 år før Thomas Jungs arbejde., af den venetianske matematiker og filosof Jacopo Ricatti.
Thomas Youngs fortjeneste ligger i, at han gav elasticitetsteorien et slankt moderne look, som efterfølgende blev formaliseret i form af en simpel og derefter generaliseret Hookes lov.
Elasticitetens fysiske karakter
Enhver krop består af atomer, mellem hvilke tiltræknings- og frastødningskræfterne virker. Balancen mellem disse kræfter erstoffets tilstand og parametre under givne forhold. Atomerne i et fast legeme begynder, når ubetydelige ydre spændings- eller kompressionskræfter påføres dem, at forskyde sig, hvilket skaber en kraft i modsat retning og af samme størrelse, som har en tendens til at bringe atomerne tilbage til deres oprindelige tilstand.
I processen med en sådan forskydning af atomer, øges energien i hele systemet. Eksperimenter viser, at ved små stammer er energien proportional med kvadratet af disse stammer. Dette betyder, at kraften, der er en afledt med hensyn til energi, viser sig at være proportional med den første potens af belastningen, det vil sige, at den afhænger lineært af den. Ved at besvare spørgsmålet, hvad er elasticitetsmodulet, kan vi sige, at dette er proportionalitetskoefficienten mellem kraften, der virker på atomet, og den deformation, som denne kraft forårsager. Dimensionen af Youngs modul er den samme som dimensionen af tryk (Pascal).
Elastisk grænse
Ifølge definitionen angiver elasticitetsmodulet, hvor meget belastning der skal påføres et fast stof, for at dets deformation er 100 %. Alle faste stoffer har dog en elastisk grænse svarende til 1 % belastning. Dette betyder, at hvis en passende kraft påføres, og kroppen deformeres med en mængde mindre end 1%, så genskaber kroppen nøjagtigt sin oprindelige form og dimensioner efter afslutningen af denne kraft. Hvis der påføres for meget kraft, ved hvilken deformationsværdien overstiger 1%, efter afslutningen af den ydre kraft, vil kroppen ikke længere genoprette sine oprindelige dimensioner. I sidstnævnte tilfælde taler man om eksistensen af en resterende deformation, dvsbevis på, at materialets elasticitetsgrænse er overskredet.
Youngs modul i aktion
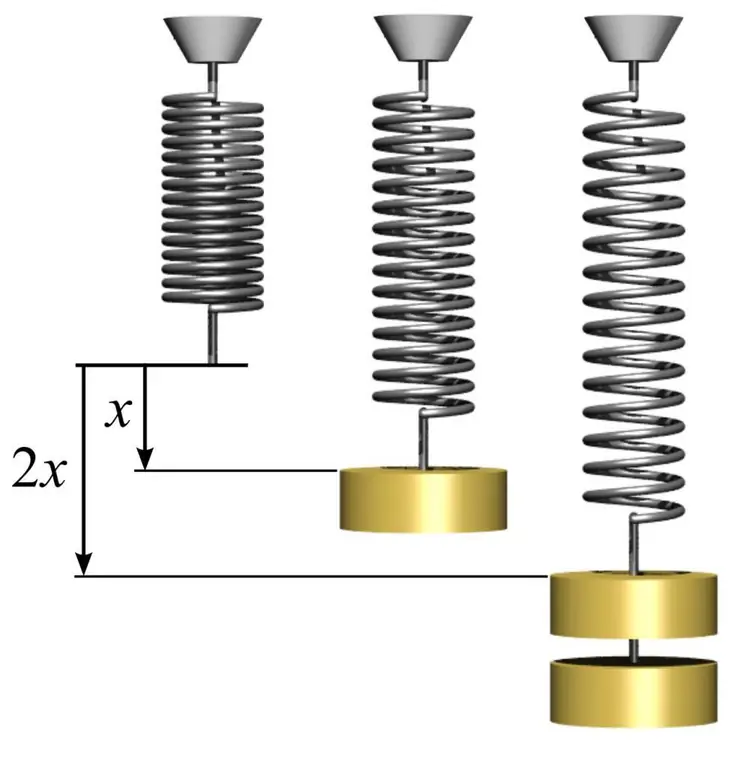
For at bestemme elasticitetsmodulet, samt for at forstå, hvordan man bruger det, kan du give et simpelt eksempel med en fjeder. For at gøre dette skal du tage en metalfjeder og måle området af cirklen, som dens spoler danner. Dette gøres ved hjælp af den simple formel S=πr², hvor n er pi lig med 3,14 og r er radius af fjederens spole.
Mål derefter længden af fjederen l0 uden belastning. Hvis du hænger en last med masse m1 på en fjeder, så vil den øge sin længde til en vis værdi l1. Elasticitetsmodulet E kan beregnes ud fra viden om Hookes lov ved hjælp af formlen: E=m1gl0/(S(l) 1-l0)), hvor g er accelerationen af det frie fald. I dette tilfælde bemærker vi, at mængden af deformation af fjederen i det elastiske område kan langt overstige 1%.
Kendskab til Young's modul giver dig mulighed for at forudsige mængden af deformation under påvirkning af en bestemt stress. I dette tilfælde, hvis vi hænger en anden masse m2 på fjederen, får vi følgende værdi af relativ deformation: d=m2g/ (SE), hvor d - relativ deformation i det elastiske område.
Isotropi og anisotropi
Elasticitetsmodul er et kendetegn ved et materiale, der beskriver styrken af bindingen mellem dets atomer og molekyler, men et bestemt materiale kan have flere forskellige Youngs moduler.
Faktum er, at egenskaberne for hvert fast stof afhænger af dets indre struktur. Hvis egenskaberne er ens i alle rumlige retninger, så taler vi om et isotropt materiale. Sådanne stoffer har en homogen struktur, så virkningen af en ekstern kraft i forskellige retninger på dem forårsager den samme reaktion fra materialet. Alle amorfe materialer er isotrope, såsom gummi eller glas.
Anisotropi er et fænomen, der er karakteriseret ved afhængigheden af de fysiske egenskaber af et fast stof eller en væske af retning. Alle metaller og legeringer baseret på dem har et eller andet krystalgitter, det vil sige et ordnet snarere end et kaotisk arrangement af ioniske kerner. For sådanne materialer varierer elasticitetsmodulet afhængigt af virkningsaksen for den ydre spænding. For eksempel har metaller med kubisk symmetri, såsom aluminium, kobber, sølv, ildfaste metaller og andre, tre forskellige Young's moduli.
Shear modulus
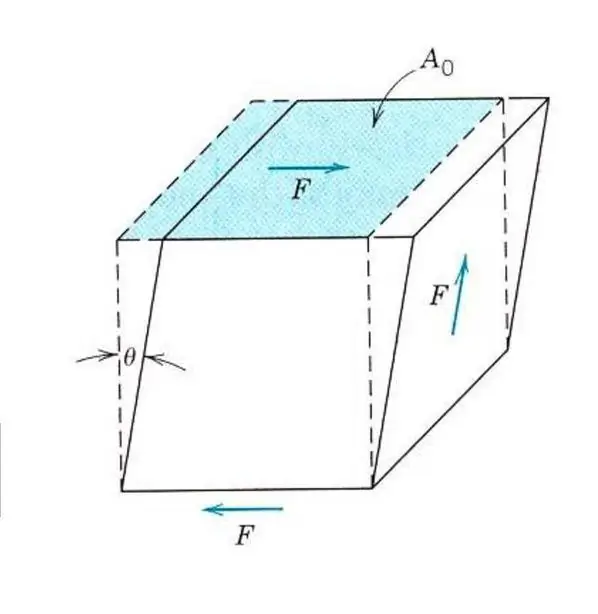
Beskrivelse af de elastiske egenskaber af selv et isotropt materiale kræver ikke kendskab til en Youngs modul. For udover spænding og kompression kan materialet blive påvirket af forskydningsspændinger eller vridningsspændinger. I dette tilfælde vil det reagere anderledes på ydre kraft. For at beskrive elastisk forskydningsdeformation introduceres en analog af Youngs modul, forskydningsmodul eller elasticitetsmodul af den anden art.
Alle materialer modstår forskydningsspændinger mindre end spænding eller kompression, så forskydningsmodulværdien for dem er 2-3 gange mindre end værdien af Youngs modul. For titanium, hvis Youngs modul er lig med 107 GPa, er forskydningsmodulet såledeskun 40 GPa, for stål er disse tal henholdsvis 210 GPa og 80 GPa.
Elasticitetsmodul af træ

Træ er et anisotropt materiale, fordi træfibre er orienteret i en bestemt retning. Det er langs fibrene, at træets elasticitetsmodul måles, da det er 1-2 størrelsesordener mindre på tværs af fibrene. Kendskab til Youngs modul for træ er vigtig og tages i betragtning ved design af træpanelstrukturer.
Værdierne for træets elasticitetsmodul for nogle typer træer er vist i tabellen nedenfor.
| Træudsigt | Youngs modul i GPa |
| Laurbærtræ | 14 |
| Eucalyptus | 18 |
| Cedar | 8 |
| gran | 11 |
| Pine | 10 |
| Oak | 12 |
Det skal bemærkes, at de angivne værdier kan variere med op til 1 GPa for et bestemt træ, da dets Young's modul er påvirket af træets tæthed og vækstbetingelser.

Forskydningsmoduler for forskellige træarter ligger i intervallet 1-2 GPa, for eksempel er det for fyr 1,21 GPa, og for eg 1,38 GPa, det vil sige, at træ praktisk t alt ikke modstår forskydningsspændinger. Denne kendsgerning skal tages i betragtning ved fremstilling af bærende trækonstruktioner, som er designet til kun at fungere i spænding eller kompression.
Elastiske egenskaber for metaller
Sammenlignet med Youngs modul af træ, er gennemsnitsværdierne for denne værdi for metaller og legeringer en størrelsesorden større, som vist i følgende tabel.
| Metal | Youngs modul i GPa |
| Bronze | 120 |
| Kobber | 110 |
| Stål | 210 |
| Titanium | 107 |
| Nikkel | 204 |
Elastiske egenskaber for metaller, der har en kubisk syngoni, er beskrevet af tre elastiske konstanter. Sådanne metaller omfatter kobber, nikkel, aluminium, jern. Hvis et metal har en sekskantet syngoni, er der allerede brug for seks konstanter til at beskrive dets elastiske egenskaber.
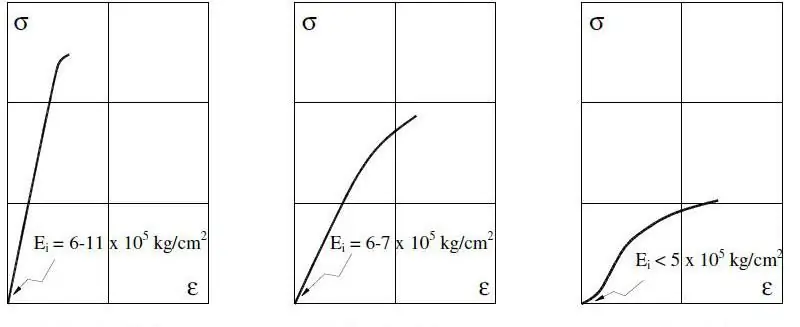
For metalliske systemer måles Youngs modul inden for 0,2 % belastning, da der allerede kan forekomme store værdier i det uelastiske område.






